Brüche kürzen und erweitern - Arbeitsblätter online rechnen
Brüche kürzen und erweitern einfach erklärt
Was versteht man unter Brüche kürzen und erweitern?
Wir starten mit einer Übung zum Einstieg!
Wir haben ein Rechteck im Bild nebenan einmal in 8 Teile eingeteilt und einmal nur in 4 Teile eingeteilt. Jedes Mal ist jedoch die gleiche Fläche in gelb eingefärbt. Wie viele Bruchteile sind es jeweils?
Ergänze die Bruchrechenaufgabe unter dem Bild!
Löse die folgenden interaktiven Aufgaben. Dann verstehst du besser, dass zwei verschiedene Brüche doch den gleichen Wert besitzen können. Diese Umformung werden wir nun genauer untersuchen. Man nennt Sie auch Brüche kürzen und erweitern.
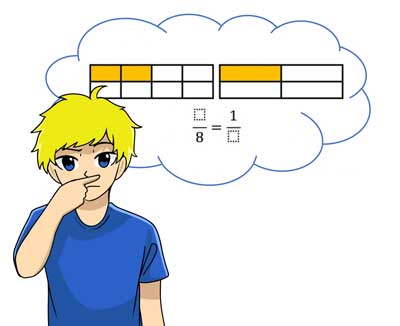
Übung 1
Ergänze die Brüche, so dass sie die Bilder darüber genau beschreiben!
Ziehe dazu die passenden Zahlen in die dafür vorgesehenen Felder!
Brüche erweitern
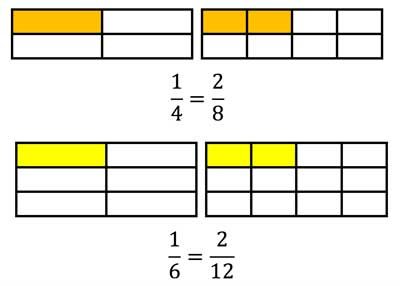
Im Bild oben lernen wir Brüche Erweitern mit 2
(Jeder Bruchteil wird dabei halbiert!)
Zähler und Nenner werden jeweils mit 2 multipliziert!
\(\frac{1}{4}=\frac{1\cdot 2}{4\cdot 2}=\frac{2}{8} \)
\(\frac{1}{6}=\frac{1\cdot 2}{6\cdot 2}=\frac{2}{12} \)
Definition – Brüche Erweitern
Erweitern eines Bruches heißt, dass wir Zähler und Nenner des Bruchs mit der gleichen Zahl multiplizieren.
Anschaulich bedeutet Erweitern, dass wir die Bruchteile jeweils alle weiter in gleicher Weise teilen.
Brüche erweitern Beispiele:
\(\frac{1}{3}=\frac{1\cdot 2}{3\cdot 2}=\frac{2}{6}=\frac{2\cdot 3}{6\cdot 3}=\frac{6}{18}\)
\(\frac{3}{8}=\frac{3\cdot 2}{8\cdot 2}=\frac{6}{16}=\frac{6\cdot 3}{16\cdot 3}=\frac{18}{48}\)
\(\frac{2}{5}=\frac{2\cdot 2}{5\cdot 2}=\frac{4}{10}=\frac{4\cdot 3}{10\cdot 3}=\frac{12}{30}\)
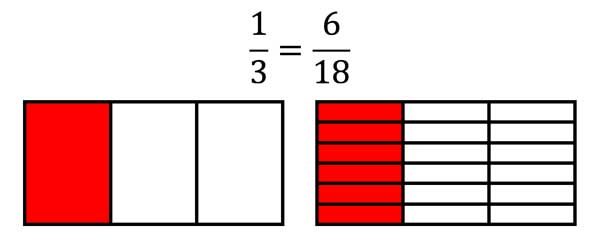
Hier wird jedes Teilstück nochmals in 6 Teile zerlegt.
Dies bedeutet Erweitern mit 6!
Brüche kürzen
Definition – Brüche Kürzen
Das Kürzen eines Bruches heißt, dass wir Zähler und Nenner des Bruchs durch die gleiche Zahl teilen.
MERKE!
Können wir Zähler und Nenner eines Bruches nicht mehr durch eine gleiche Zahl teilen, sprechen wir davon, dass der Bruch vollständig gekürzt ist.
Damit wir den Zähler und den Nenner eines Bruchs durch die gleiche Zahl teilen können, müssen wir sehr genau prüfen, durch welche Zahlen Zähler und Nenner überhaupt teilbar sind. Dazu müssen wir die Teilbarkeitsregeln und die Primfaktorzerlegung anwenden können!
Brüche kürzen Beispiele:
\(\frac{6}{18}=\frac{6:3}{18:3}=\frac{2}{6} =\frac{2:2}{6:2}=\frac{1}{3} \)
\(\frac{42}{60}=\frac{42:6}{60:6}=\frac{7}{10} \)
\(\frac{48}{80}=\frac{48:8}{80:8}=\frac{6}{10} =\frac{6:2}{10:2}=\frac{3}{5} \)
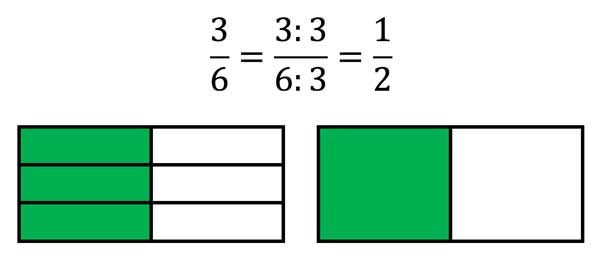
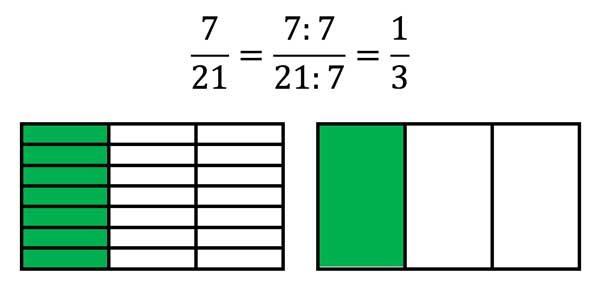
In den Bildern oben lernen wir Brüche Kürzen mit 3 und mit 7.
Immer 3 bzw. immer 7 Teile werden zu einem Teil zusammengefasst. Das geht natürlich nur, wenn die gesamte Anzahl aller Teile durch 3 oder durch 7 teilbar ist.
Die Primfaktorzerlegung um Brüche zu kürzen
Das Kürzen von Brüchen wird besonders einfach, wenn wir den Zähler und den Nenner des Bruchs in Primfaktoren zerlegen. Dann können wir gemeinsame Faktoren im Zähler und Nenner einfach durchstreichen. Brüche kürzen wir mit dieser Methode vollständig!
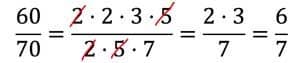
Wenn du noch Probleme mit der Primfaktorzerlegung hast, besuche unsere Seite zur Teilbarkeit und Primfaktorzerlegung und benutze den online Rechner zur Primfaktorzerlegung!
Hast du die Methode des vollständigen Kürzens mit der Primfaktorzerlegung verstanden?
Mache die kleine online Übung, um es zu testen!
Gehe wie folgt vor:
- Zerlege Zähler und Nenner in Primfaktoren!
- Lasse gemeinsame Faktoren weg!
- Trage alle restlichen Faktoren wieder ein!
- Notiere die Zahlen immer in aufsteigender Reihenfolge (von klein nach groß)
Brüche kürzen und erweitern - online Aufgaben
Wir üben Brüche erweitern!
Beachte den Hinweis zum Ausfüllen:
Trage in die leeren Felder bei A den Wert für den Zähler und bei B den Wert für den Nenner ein. Leider kann das online Tool für die Aufgabe diese Eingabe nicht direkt auf bzw. unter dem Bruchstrich darstellen!
Beispiel – So rechnest du die Aufgaben in der online Übung:
\( \frac{1}{2} \overset{ \cdot \text{10}}{=} \frac{A}{B}\) A = 10 B = 20\( \frac{12}{15} \underset{ \text{:3}}{=} \frac{A}{B}\) A = 4 B = 5Übung 1 – Brüche erweitern
a) Erweitere alle Brüche mit 3!
b) Erweitere alle Brüche mit 5!
c) Erweitere alle Brüche mit 8!
Übung 2 – Brüche kürzen – einfach
Kürze NUR mit der Zahl die unter dem Gleichzeichen angegeben ist!
a) Kürze den Bruch mit dem größten gemeinsamen Teiler.
In dieser Aufgabe a) steht der gemeinsame Teiler noch unter dem Gleichzeichen!
b) Kürze vollständig, so dass Zähler und Nenner keinen gemeinsamen Teiler mehr haben!
Nur vollständig gekürzt ist das Ergebnis richtig!
c) Kürze vollständig, so dass Zähler und Nenner keinen gemeinsamen Teiler mehr haben!
d) Kürze vollständig, so dass Zähler und Nenner keinen gemeinsamen Teiler mehr haben!
Memospiele: Finde gleiche Bruchteile gekürzt oder erweitert
Memospiele – Brüche kürzen und erweitern
Finde Brüche mit dem gleichen Wert! Dazu musst du einen Bruch erweitern oder kürzen, um einen gleichwertigen Bruch zu finden.
Memospiel 1
Das Buch mit vielen Bruchrechnen Aufgaben: "Mathestunde 5 - Einfache Bruchteile"
Das Übungsheft zum Einstieg in die Bruchrechnung, viele Aufgaben zu Brüche Kürzen und Erweitern in einem Heft!
Mathestunde 5 – Einfache Bruchrechnung
Übungsheft für die 5. Klasse / 6. Klasse
- Umfang: 60 Seiten, DIN A 4, geheftet, s/w
- Erschienen: 2015
- ISBN: 978-394186817-5
- Preis: 5,95 €
- Überall erhältlich in jeder Buchhandlung (bestellbar) oder in online Shops.

