Brüche in Dezimalzahlen umwandeln - Aufgaben & online Übungen
Brüche in Dezimalzahlen umwandeln - Einstieg und Wiederholung
Brüche in Dezimalzahlen umwandeln
Dezimalzahlen in Brüche umwandeln
Wie rechnet man mit Dezimalzahlen oder Dezimalbrüchen?
In diesem Abschnitt lernen wir, wie man Dezimalbrüche in Brüche umwandeln kann und wie man mit diesen Dezimalbrüchen rechnet. Beim Rechnen mit Größen sind uns viele Begriffe schon begegnet.
- 1 Dezimeter = 1 Zehntel Meter = \( \frac {1}{10} m \)
- 1 Zentimeter = 1 Hundertstel Meter = \( \frac {1}{100} m \)
- 1 Millimeter = 1 Tausendstel Meter = \( \frac {1}{1000} m \)

wie man mit Dezimalzahlen rechnet.
Übung 1 zum Start: Bruchteile und Komma Schreibweise
Ziehe die richtige Lösung an die dafür vorgesehenen Felder!

b) Brüche in Komma Schreibweise mit Dezimalzahlen
Ziehe die Dezimalzahlen an die richtige Stelle!
Dezimalbrüche Übungen 1 - Längen umrechnen

einfach ausdrucken oder
digital bearbeiten!
Arbeitsblätter Dezimalbrüche
Diese Aufgaben als PDF zum Ausdrucken:
Wähle im TOP-Menü die Sprache, um die richtige Sprache auf dem Arbeitsblatt zu erhalten!
Wir wandeln Brüche in Dezimalzahlen um
So kannst du Brüche in Dezimalzahlen umwandeln
Alle Brüche mit einer Zehnerpotenz im Nenner können als Dezimalbruch oder Dezimalzahl geschrieben werden!Beispiele:Steht im Nenner noch keine Zehnerzahl (Zehnerpotenz), gilt die folgende Regel:Kannst du den Nenner eines Bruchs durch Kürzen oder Erweitern auf eine Zehnerpotenz (Zehnerzahl 10, 100, 1000, …) bringen, dann kann man den Bruch auch als Dezimalbruch schreiben.einige Beispiele:
Dezimalzahlen wieder in Brüche umwandeln
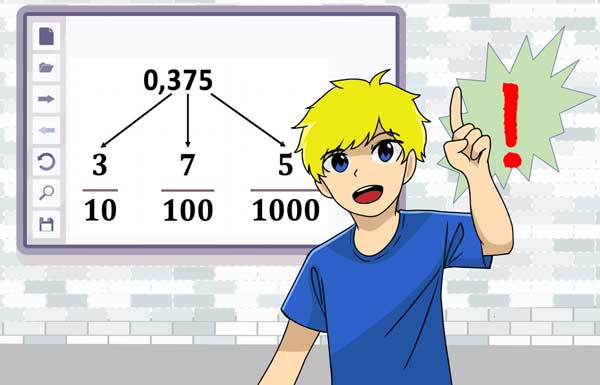
1. Stelle = Zehntel, 2. Stelle = Hundertstel, 3. Stelle = Tausendstel, ...
Die Stellen hinter dem Komma haben eine Bedeutung!
Siehe im Beispiel: Die Zahl 0,375
0,3 = 3 Zehntel
0,07 = 7 Hundertstel
0,005 = 5 Tausendstel
0,375 = 3 Zehntel + 7 Hundertstel + 5 Tausendstel
oder:
\(\frac{3}{10} \overset{ \cdot \text{10}}{=}\frac{30}{100} \overset{ \cdot \text{10}}{=}\frac{300}{1000} \)\(\frac{7}{100} \overset{ \cdot \text{10}}{=}\frac{70}{1000}\)0,375 = \( \frac{300}{1000} + \frac{70}{1000} + \frac{5}{1000} = \frac{375}{1000}\)
So gehst du vor bei der Umwandlung von einer Dezimalzahl in einen Bruch:
Stelle fest, wie viele Stellen hinter dem Komma sind.
Diese Stellen geben dir an, welche Zahl in den Nenner gehört:
- bei nur 1 Stelle: 10 (Zehntel)
- bei 2 Stellen: 100 (Hundertstel)
- bei 3 Stellen: 1 000 (Tausendstel)
- bei 4 Stellen: 10 000 (Zehntausendstel)
- immer so weiter!
Alle Zahlen vor und hinter dem Komma kommen dann auf den Bruchstrich, also in den Zähler des Bruchs.
Beispiele:
(1) 2,705 => 3 Stellen hinter dem Komma = Tausendstel! alle Ziffern in den Zähler, 1000 in den Nenner: \( 2,705 = \frac{2705}{1000}\)
(2) 0,0074 => 4 Stellen hinter dem Komma = Zehntausendstel! Alle Ziffern in den Zähler, 10 000 in den Nenner: \( 0,0074 = \frac{74}{10000}\)
Alles klar?
Dann kann es mit weiteren Übungen losgehen.
Aufgaben - online oder als PDF ausdrucken
- Schreibe als Dezimalbruch!
Brüche in Dezimalzahlen umwandeln (2)
- Schreibe als Dezimalbruch!
Dezimalbrüche Übungen (3)
- Wandle die Dezimalbrüche in Brüche um und kürze das Ergebnis soweit wie möglich!

einfach ausdrucken oder
digital bearbeiten!
4 Arbeitsblätter Dezimalbrüche
Die Aufgaben aus diesen 4 Übungen als PDF zum Ausdrucken:
Wähle im TOP-Menü die Sprache, um die richtige Sprache auf dem Arbeitsblatt zu erhalten!
Dezimalbrüche Aufgaben online (4)
- Wandle die Brüche in Dezimalzahlen um. Hierzu musst du den Bruch vorher kürzen oder erweitern.
Finde die Paare - Brüche und Dezimalbrüche mit dem gleichen Wert
Das Buch mit vielen Aufgaben zur Bruchrechnung: "Mathestunde 5 - Einfache Bruchteile"
Das Übungsheft zum Einstieg in die Bruchrechnung, mit vielen Dezimalbrüche Aufgaben in einem Heft!
Mathestunde 5 – Einfache Bruchrechnung
Übungsheft für die 5. Klasse / 6. Klasse
- Umfang: 60 Seiten, DIN A 4, geheftet, s/w
- Erschienen: 2015
- ISBN: 978-394186817-5
- Preis: 5,95 €
- Überall erhältlich in jeder Buchhandlung (bestellbar) oder in online Shops.

