Calculate area rectangle - interactive tasks rectangle
Rectangle area
Master area rectangle
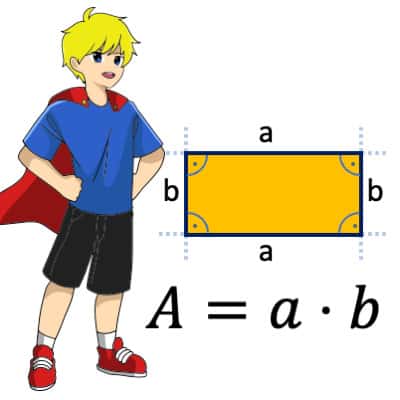
To calculate the area of a rectangle, let's first consider a rectangle.
The rectangle
A rectangle is a geometric figure consisting of four sides. It is a special type of quadrilateral in which all interior angles are 90 degrees. This means that the sides that meet form a right angle (90 degrees). Opposite sides are of the same length in the rectangle.
Similarly, it means that a rectangle has two pairs of parallel sides, each of which is the same length, while the other two sides are also the same length.
The length of the longer side of a rectangle is often called the "length", while the length of the shorter side is often called the "width".
The properties of the rectangle make it a useful geometric shape in many practical applications, including construction, commerce, agriculture, surveying, and geometry.
You can find more information about the rectangle at Wikipedia: https: //de.wikipedia.org/wiki/Rechteck
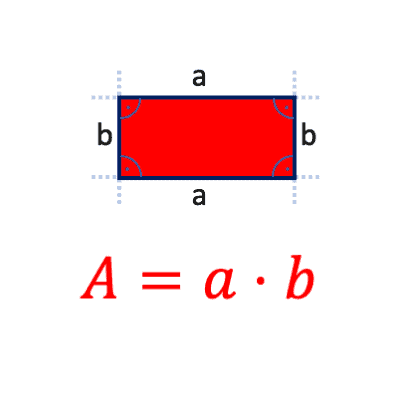
Calculate area of rectangle
We calculate the area of a rectangle by simply multiplying the length (also called the "side length" or "side dimension", we take the letter a) by the width (also called the "side length" or "side dimension", we take the letter b).
Area rectangle formula
The formula for the area of a rectangle is :
Area = \(length \cdot width = a \cdot b \)
Sometimes the abbreviation "A" is also used for the area. In this case the formula is:
\( A = a \cdot b \) or \( A = l \cdot b \)
For example, a rectangle with a length of 5 cm and a width of 3 cm has an area of:
Area = \( 5 cm \cdot 3 cm = 15 cm^2 \)
The area of the rectangle in our example is 15 square centimeters.
When calculating areas with lengths, it is important that each length has a unit of length, such as cm (centimeter). Then the unit of area is cm x cm = cm^2 = square centimeter
Area rectangle calculator
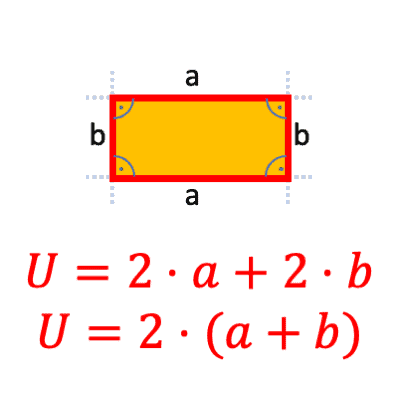
Calculate perimeter rectangle
How to calculate the perimeter of a rectangle
The perimeter of a rectangle is the length of the boundary line surrounding all four sides of the rectangle. To calculate the perimeter of a rectangle, simply add the lengths of all four sides together.
Perimeter rectangle formula
The formula for the perimeter of a rectangle is:
Scope = \( 2 \cdot a + 2 \cdot b = 2 \cdot (a + b) \)
where a = the length of the rectangle and b is the width of the rectangle.
For example, a rectangle with a length of a = 8 cm and a width of b = 5 cm has a perimeter of:
Circumference \( = 2 \cdot (8 cm + 5 cm) = 2 \cdot 13 cm = 26 cm \)
The perimeter of the rectangle is U = 26 cm (centimeters).
Perimeter rectangle calculator
Rectangle tasks interactive
Interactive tasks for the area of a rectangle
Rectangle and square the info poster as PDF
Mnemonic - Square and Rectangle
Square and rectangle fact sheet
Definitions:
- A square is a special rectangle where all four sides are the same length.
- The rectangle is a geometric shape with four sides and four angles, where opposite sides are equal in length and all angles measure 90 degrees.
Features:
- Square: sides of equal length, angles of equal size, diagonal length = side length * square root of 2
- Rectangle: opposite sides are equal in length, opposite angles are equal in size, diagonal length = square root of (side length^2 + side width^2)
Formulas:
- Area of the square: side length^2
- Perimeter of the square: 4 * side length
- Area of the rectangle: side length * side width
- Perimeter of the rectangle: 2 * (side length + side width)
Examples:
- A classic chessboard has 64 squares, all of which are square.
- A window can be modeled as a rectangle to calculate its dimensions and size.
Exercises:
- Calculate the area and perimeter of a square with sides 5 cm long.
- Calculate the area and perimeter of a rectangle with sides 6 cm long and 4 cm wide.
- Draw a rectangle with an area of 20 cm² and determine its dimensions.
Mnemonics:
- A square has 4 sides of equal length.
- Diagonals of squares and rectangles can be calculated by substituting the side lengths into a formula.
- The formula for the perimeter of a rectangle is: 2 * (side length + side width).
Applications:
- Architects use square and rectangular shapes when designing buildings.
- Designers use these shapes in the design of furniture and other objects.
- In geometry, square and rectangular shapes are an important part of the study of shapes and surfaces.
Summary:
- Square: All sides are the same length, area = side length^2, perimeter = 4 * side length
- Rectangle: opposite sides are of equal length, area = side length * side width, perimeter = 2 * (side length + side width)
- Diagonals can be calculated by inserting the side lengths into a formula.
- Square and rectangular shapes have applications in architecture, design and geometry.
We have compiled the most important information about square and rectangle on our info poster!
Area calculation of rectangles - where do you need it?
The calculation of the area of rectangles is used in many areas of practice. Here are just a few examples:
- Construction: When constructing buildings or structures, architects and engineers must calculate the area of rectangles to determine the amount of materials, such as wood, concrete, tile, or paint, needed for construction.
- Trade: In trade, the calculation of the area of rectangles is used to determine the price of products sold based on their size or coverage. Examples include carpets, floor coverings, and wall tiles.
- Agriculture: When planning and managing agricultural land, the size of fields, pastures, and cropland must be calculated to determine the amount of seed, fertilizer, and pesticides needed.
- Surveying: Surveyors use the area calculation of rectangles to survey land boundaries, determine property size, or determine the area of buildings or other structures.
- Geometry: The calculation of the area of rectangles is also important in geometry, as it forms an important basis for the calculation of areas of other shapes such as triangles, trapezoids and circles.
These examples show how important the calculation of the area of rectangles is in many areas of practice.




