Convert fractions to decimals - tasks & online exercises
Convert fractions to decimals - introduction and repetition
Convert fractions to decimal numbers
Convert decimal numbers to fractions
How do you calculate with decimal numbers or decimal fractions?
In this section we learn how to convert decimal fractions into fractions and how to calculate with these decimal fractions. When calculating with quantities, we have already encountered many terms.
- 1 decimetre = 1 tenth of a metre = \( \frac {1}{10} m \)
- 1 centimetre = 1 hundredth of a metre = \( \frac {1}{100} m \)
- 1 millimetre = 1 thousandth of a metre = \( \frac {1}{1000} m \)

how to calculate with decimal numbers.
Exercise 1 to start: Fractions and comma notation
Drag the correct solution to the spaces provided!

b) Fractions in comma notation with decimal numbers
Drag the decimal numbers to the right place!
Decimal fractions Exercises 1 - Convert lengths

simply print or
digitally edit!
Worksheets Decimal Fractions
These tasks as a PDF for printing:
Select the language in the TOP menu to get the correct language on the worksheet!
We convert fractions into decimal numbers
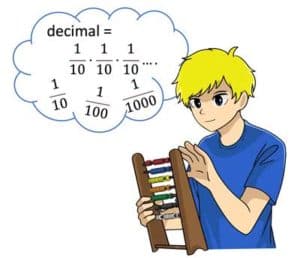
How to convert fractions into decimal numbers
All fractions with a power of ten in the denominator can be written as a decimal fraction or decimal number!Examples:If there is no number of tens (power of ten) in the denominator, the following rule applies:If you can reduce or expand the denominator of a fraction to a power of ten (tens 10, 100, 1000, ...), then the fraction can also be written as a decimal fraction.some examples:
Convert decimal numbers back to fractions
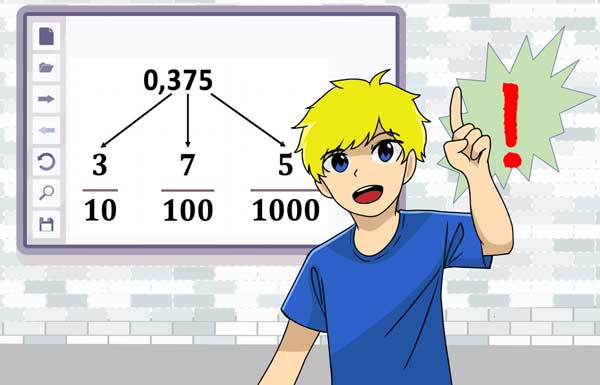
1st digit = tenths, 2nd digit = hundredths, 3rd digit = thousandths, ...
The digits after the comma have a meaning!
See in the example: The number 0.375
0.3 = 3 tenths
0.07 = 7 hundredths
0.005 = 5 thousandths
0.375 = 3 tenths + 7 hundredths + 5 thousandths
or:
\(\frac{3}{10} \overset{ \cdot \text{10}}{=}\frac{30}{100} \overset{ \cdot \text{10}}{=}\frac{300}{1000} \)
\(\frac{7}{100} \overset{ \cdot \text{10}}{=}\frac{70}{1000}\)
0.375 = \( \frac{300}{1000} + \frac{70}{1000} + \frac{5}{1000} = \frac{375}{1000}\)
This is how you convert a decimal number into a fraction:
Determine how many digits are behind the decimal point.
These digits tell you which number belongs in the denominator:
- with only 1 digit: 10 (tenths)
- with 2 digits: 100 (hundredths)
- with 3 digits: 1 000 (thousandth)
- with 4 digits: 10 000 (ten thousandths)
- keep it up!
All numbers before and after the decimal point are then placed on the fraction line, i.e. in the numerator of the fraction.
Examples:
(1) 2,705 => 3 Stellen hinter dem Komma = Tausendstel! alle Ziffern in den Zähler, 1000 in den Nenner: \( 2,705 = \frac{2705}{1000}\)
(2) 0,0074 => 4 Stellen hinter dem Komma = Zehntausendstel! Alle Ziffern in den Zähler, 10 000 in den Nenner: \( 0,0074 = \frac{74}{10000}\)
All right?
Then we can start with more exercises.
Tasks - print online or as PDF
- Write as a decimal fraction!
Convert fractions to decimal numbers (2)
- Write as a decimal fraction!
Decimal fractions exercises (3)
- Convert the decimal fractions into fractions and shorten the result as much as possible!

simply print or
digitally edit!
4 worksheets decimal fractions
The tasks from these 4 exercises as a PDF to print out:
Select the language in the TOP menu to get the correct language on the worksheet!
Decimal fractions tasks online (4)
- Convert the fractions into decimal numbers. To do this, you have to shorten or expand the fraction first.
Find the pairs - fractions and decimal fractions with the same value
The book with many tasks for fractions: "Maths lesson 5 - Simple fractions".
The exercise book for getting started with fractions, with many decimal fractions tasks in one booklet!
Maths lesson 5 - Simple fractions
Exercise book for 5th grade / 6th grade
- Length: 60 pages, DIN A 4, stitched, b/w
- Published: 2015
- ISBN: 978-394186817-5
- Price: 5,95 €
- Available everywhere in every bookshop (orderable) or in online shops.

