Prime numbers up to 100 & prime factorisation online

What is a prime number - prime number definition

Here we answer important questions about prime numbers. In the further course of this page, we will deal with the questions in more detail!

Definition prime number

A prime number is a number that is only divisible by 1 and itself. The smallest prime number and also the only prime number that is even is TWO (2)!

This number is usually forgotten because it is an even number. All other prime numbers are odd numbers, because otherwise they would also be divisible by 2, except by themselves and 1!

What is meant by prime factorisation?

You can divide any number into factors. Exception: it is a prime number, then the number is only divisible by 1 and itself, which means that as a product it can only be written as 1 times itself.

What are the prime numbers up to 100?

List of all prime numbers between 1 and 100:

How do you do a prime factorisation?

A prrim factorisation is done by applying the divisibility rules. If the number is divisible, you start again from the beginning. Many calculators can "factorise" and thus perform a prime factorisation. Or you can use our online decomposition calculator!

Why do you need prime numbers and the prime factorisation?

Reduce fractions

At school, you need the prime factorisation in fractions in order to completely reduce fractions. Numerator and denominator are decomposed into prime factors. Common factors in the numerator and denominator can be deleted (shortened).

An indispensable part of the computer world: encryption with prime numbers

Prime numbers are important for encryption, especially in modern cryptography, for two main reasons:

Key generation: In many encryption algorithms, especially in asymmetric encryption methods such as the RSA algorithm (Rivest-Shamir-Adleman), prime numbers are used to generate key pairs. These key pairs consist of a public key (used to encrypt data) and a private key (used to decrypt data). The security of such encryption algorithms is based on the difficulty of factorizing large prime numbers, especially when they are the product of two large prime numbers. Since factoring large numbers is a time-consuming process, using prime numbers provides high security for encryption.
Security: Prime numbers also play an important role in other cryptographic protocols and techniques, such as digital signatures and key exchange procedures. They provide a mathematical basis for the security of encryption systems, since the calculation of the private key from the public key can often be traced back to the factoring of large numbers.

If you want to learn more about it, just click on the link and read a little at wikipedia (RSA) about it!

1 to 100 - How many prime numbers are there?

You should know the first prime numbers, maybe even all prime numbers up to 100, by heart. At least up to 20 or even better all Prime numbers up to 100. There are 25 prime numbers in the set of natural numbers up to 100!

In primary school, you learned the multiplication tables and thus many numbers that can be decomposed into a drawing task from the 1×1.

Examples are:

\(35 = 5\cdot 7 \)
\(56 = 7\cdot 8 = 7 \cdot 2 \cdot 2 \)
\(63 = 7\cdot 9 = 7 \cdot 3 \cdot 3 \)

If you all numbers from the 1×1 you will see many numbers in the 100s table or hundreds table that do not belong to it. But not all numbers that do not appear in the multiplication table are prime numbers. All the other numbers in the multiplication table are multiples of smaller prime numbers, e.g.

\(22 =2 \cdot 11 \)
\(57 = 3\cdot 19 \)
\(92 = 4\cdot 23 \)

But you can also see 57 as a number in the continuation of the row of 3, namely in the 19th place.

List of all prime numbers up to 100:

2, 3, 5, 7, 11, 13, 17, 19,

23, 29, 31, 37,

41, 43, 47, 53, 59,

61, 67, 71, 73, 79,

83, 89, 97

Prime numbers - in the hundreds table

The prime numbers can also be marked in the hundreds table.

Pay attention to the colours in the table of numbers up to 100!

all numbers from the 1×1 (without the prime numbers up to 10: 2,3,7)
Multiples of prime numbers
the prime numbers up to 100

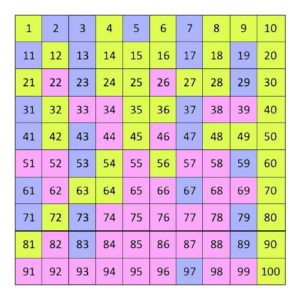
All numbers up to 100, marked in colour.

Prime numbers in this colour!

Which numbers are prime numbers - calculate with the prime factorisation

How many prime numbers are there - try it out with the online prime number decomposition

Prime factorisation online

We have written a small programme that can decompose numbers into prime factors. Try it out. The input does not yet check whether it is a valid number. Therefore, you must make sure that only numbers are entered into the field!

Enter the number to be decomposed in the following field:

Prime numbers up to 100 - the prime factorisation

To help you understand prime factorisation better, we have broken down all numbers from 1 to 100 into prime factors here, as far as it is possible.

1 - 25 - the prime factorisation

1 – 25

\(1=1 \cdot 1 \) not a prime number
\( 2 = 1\cdot 2 \) prime number
\( 3 = 1\cdot 3 \) prime number
Prime factorisation 4 \( = 2\cdot 2 =2^2\)
\(5 = 1\cdot 5 \) prime number
Prime factorisation 6 \( = 2\cdot 3 \)
\(7 = 1\cdot 7 \) prime number
Prime factorisation 8 \( = 2\cdot 2 \cdot 2=2^3\)
Prime factorisation 9 \( = 3\cdot 3=3^2 \)
Prime factorisation 10 \( = 2\cdot 5 \)
\(11 = 1\cdot 11 \) prime number
Prime factorisation 12 \( = 2\cdot 2 \cdot 3 \)
\(13 = 1 \cdot 13 \) prime number
Prime factorisation 14 \( = 2\cdot 7 \)
Prime factorisation 15 \( = 3\cdot 5 \)
Prime factorisation 16 \( = 2\cdot 2 \cdot 2 =2^4\)
\(17 = 1 \cdot 17\) prime number
Prime factorisation 18 \( = 2\cdot 3 \cdot 3 \)
\(19 = 1\cdot 19 \) prime number
Prime factorisation 20 \( = 2\cdot 2 \cdot 5 \)
Prime factorisation 21 \( = 3\cdot 7 \)
Prime factorisation 22 \( = 2\cdot 11 \)
\(23 = 1 \cdot 23 \) prime number
Prime factorisation 24 \( = 2\cdot 2\cdot 2 \cdot 3 \)
Prime factorisation 25 \( = 5\cdot 5=5^2 \)

Prime factorisation up to 50

26 – 50

Prime factorisation 26 \(=2\cdot 13 \)
Prime factorisation 27 \( = 3\cdot 3 \cdot 3 \)
Prime factorisation 28 \( = 2\cdot 2 \cdot 7 \)
\(29 = 1\cdot 29 \) prime number
Prime factorisation 30 \( = 2\cdot 3 \cdot 5 \)
\(31 = 1\cdot 31 \) prime number
Prime factorisation 32 \( = 2\cdot 2 \cdot 2 \cdot 2 =2^5\)
Prime factorisation 33 \( = 3\cdot 11\)
Prime factorisation 34 \( = 2\cdot 17 \)
Prime factorisation 35 \( = 5\cdot 7 \)
Prime factorisation 36 \( = 6\cdot 6=6^2 \)
\(37= 1\cdot 37\) prime number
Prime factorisation 38\( = 2 \cdot 19 \)
Prime factorisation 39 \( = 3\cdot 13 \)
Prime factorisation 40 \( = 2\cdot 2 \cdot 2 \cdot 5\)
\(41 = 1\cdot 41 \) prime number
Prime factorisation 42 \(= 2 \cdot 3 \cdot 7\)
\(43 = 1\cdot 43 \) prime number
Prime factorisation 44 \( = 2\cdot 2 \cdot 11\)
Prime factorisation 45 \( = 3\cdot 3 \cdot 9 \)
Prime factorisation 46 \( = 2\cdot 23 \)
\(47 = 1\cdot 47 \) prime number
Prime factorisation 48 \( = 2 \cdot 2 \cdot 2 \cdot 3 \)
Prime factorisation 49 \( = 7\cdot 7=7^2 \)
Prime factorisation 50 \( = 2\cdot 5\cdot 5 \)

The prime factorisation up to 75

51 – 75

\(51 = 3\cdot 17 \)
\(52 = 2\cdot 2 \cdot 13 \)
\(53 = 1\cdot 53 \) prime number
\(54 = 2\cdot 3 \cdot 3 \)
\(55 = 5\cdot 11 \)
\(56 = 2\cdot 2 \cdot 7 \)
\(57 = 3\cdot 19 \)
\(58 = 2\cdot 29 \)
\(59 = 1\cdot 59 \) prime number
\(60 = 2\cdot 2 \cdot 3 \cdot 5 \)
\(61 = 1\cdot 61 \) prime number
\(62 = 2\cdot 31 \)
\(63 = 3 \cdot 3 \cdot 7 \)
\(64=2\cdot 2 \cdot 2 \cdot 2 \cdot 2 =2^6\)
\(65 = 5\cdot 13 \)
\(66 = 2\cdot 3 \cdot 11\)
\(67 = 1\cdot 67 \) prime number
\(68 = 2\cdot 2 \cdot 17 \)
\(69 = 3\cdot 23 \)
\(70 = 2\cdot 5 \cdot 7 \)
\(71 = 1\cdot 71 \) prime number
\(72 = 2\cdot 2 \cdot 3 \cdot 3 \)
\(73 = 1\cdot 73 \) prime number
\(74 = 2\cdot 37\)
\(75 = 3\cdot 5 \cdot 5 \)

76 to 100 Prime factorisation

76 – 100

\(76 = 2\cdot 2 \cdot 19 \)
\(77 = 7\cdot 11\)
\(78 = 2\cdot 3 \cdot 13 \)
\(79 = 1\cdot 79\) prime number
\(80 = 2\cdot 2 \cdot 2 \cdot 2 \cdot 5 \)
\(81 = 3\cdot 3 \cdot 3=3^4\)
\(82 = 2\cdot 41 \)
\(83 = 1\cdot 83 \) prime number
\(84 = 2 \cdot 2\cdot 3 \cdot 7 \)
\(85 = 5 \cdot 17 \)
\(86= 2 \cdot 43 \)
\(87 = 3 \cdot 29 \)
\(88 = 2 \cdot 2 \cdot 11 \)
\(89 = 1 \cdot 89 \) prime number
\(90 = 2 \cdot 3 \cdot 5 \)
\(91 = 7 \cdot 13 \)
\(92 = 2 \cdot 2\cdot 23 \)
\(93 = 3 \cdot 31 \)
\(94 = 2 \cdot 47 \)
\(95 = 5 \cdot 19 \)
\(96 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \)
\(97 = 1 \cdot 97 \) prime number
\(98 = 2 \cdot 7\cdot 7 \)
\(99 = 3 \cdot 3\cdot 11 \)
\(100 = 2 \cdot 2\cdot 5 \cdot 5 \)

Prime numbers - How to recognise them with the divisibility rules

Prime factorisation by hand - by mental arithmetic and divisibility rules

If you want to divide a number into factors even without a computer, you need to know some divisibility rules.

We list the most important ones here:

Divisibility by 2

You've known the simplest one since primary school: Every even number is divisible by 2!

Divisibility by 3

If the cross sum of a number is divisible by 3, the number is divisible by 3!

Divisibility by 4

If a number is divisible by 2 twice or a number divided by 2 is still even, then it is divisible by 4.
Alternatively, the following also applies: if the number formed by the last 2 digits (ones and tens) is divisible by 4, then the number is divisible by 4. It is then true that the other digits from the 3rd digit onwards are hundreds. Because all hundreds are divisible by 4 (\( 100 = 4 \cdot 25 \)).

Divisibility by 5

A number is divisible by 5 if the last digit is a 5 or 0.

Divisibility by 6

An even number whose checksum is divisible by 3 is divisible by 6.
The above rule includes the rules for divisibility by 2 and by 3.

Divisibility by 9

A number is divisible by 9 if the cross sum is divisible by 9.

Prime number crossword

A prime number crossword is in preparation here!