Primzahlen bis 100 & Primfaktorzerlegung online
Was ist eine Primzahl - Primzahlen Definition
Hier beantworten wir dir wichtige Fragen zum Thema Primzahlen. Im weiteren Verlauf dieser Seite behandeln wir die Fragen dann ausführlicher!
Definition Primzahl
Eine Primzahl ist eine Zahl, die nur durch 1 und sich selbst teilbar ist. Die kleinste Primzahl und auch einzige Primzahl, die gerade ist, ist die ZWEI (2)!
Diese Zahl wird meistens vergessen, da es ja eine gerade Zahl ist. Alle anderen Primzahlen sind ungerade Zahlen, da sie ansonsten ja auch noch durch 2 teilbar wären, außer durch sich selbst und 1!
Was versteht man unter der Primfaktorzerlegung?
Du kannst jede Zahl in Faktoren zerlegen. Ausnahme: es ist eine Primzahl, dann ist die Zahl ja nur durch 1 und sich selbst teilbar, das heißt, dass man sie als Produkt auch nur als 1 mal sich selbst geschrieben werden kann.
Wie lauten die Primzahlen bis 100?
Liste aller Primzahlen zwischen 1 und 100:




Wie macht man eine Primfaktorzerlegung?
Eine Prrimfaktorzerlegung macht man, indem man die Teilbarkeitsregeln anwendet. Ist die Zahl teilbar, beginnt man wieder von Vorne. Viele Taschenrechner können “Faktorisieren” und damit eine Primfaktorzerlegung durchführen. Oder die verwendest unseren online Zerlegungsrechner!
Wozu braucht man Primzahlen und die Primfaktorzerlegung?
- Brüche kürzen
In der Schule brauchst du die Primfaktorzerlegung in der Bruchrechnung, um Brüche vollständig zu kürzen. Zähler und Nenner werden in Primfaktoren zerlegt. Gemeinsame Faktoren im Zähler und Nenner können gestrichen (gekürzt) werden.
- In der Computerwelt nicht mehr wegzudenken: Verschlüsselung mit Primzahlen
Primzahlen sind für die Verschlüsselung wichtig, insbesondere in der modernen Kryptographie, aus zwei Hauptgründen:
Schlüsselerzeugung: In vielen Verschlüsselungsalgorithmen, insbesondere in asymmetrischen Verschlüsselungsverfahren wie dem RSA-Algorithmus (Rivest-Shamir-Adleman), werden Primzahlen verwendet, um Schlüsselpaare zu erzeugen. Diese Schlüsselpaare bestehen aus einem öffentlichen Schlüssel (zur Verschlüsselung von Daten) und einem privaten Schlüssel (zur Entschlüsselung von Daten). Die Sicherheit solcher Verschlüsselungsalgorithmen basiert auf der Schwierigkeit, große Primzahlen zu faktorisieren, insbesondere wenn sie das Produkt zweier großer Primzahlen sind. Da das Faktorisieren großer Zahlen ein zeitaufwendiger Prozess ist, bietet die Verwendung von Primzahlen eine hohe Sicherheit für die Verschlüsselung.
Sicherheit: Primzahlen spielen auch eine wichtige Rolle in anderen kryptografischen Protokollen und Techniken, wie digitalen Signaturen und Schlüsselaustauschverfahren. Sie stellen eine mathematische Grundlage für die Sicherheit von Verschlüsselungssystemen dar, da die Berechnung des privaten Schlüssels aus dem öffentlichen Schlüssel oft auf das Faktorisieren von großen Zahlen zurückgeführt werden kann.
Wenn du mehr darüber erfahren willst, klicke einfach auf den Link und lies ein wenig bei wikipedia (RSA) nach!
1 bis 100 - Wie viele Primzahlen gibt es?
Die ersten Primzahlen, vielleicht sogar alle Primzahlen bis 100 solltest du auswendig kennen. Mindestens bis 20 oder sogar besser alle Primzahlen bis 100. Es gibt 25 Primzahlen in der Menge der natürlichen Zahlen bis 100!
In der Grundschule hast du das kleine Einmaleins gelernt und damit schon viele Zahlen, die in eine Malaufgabe aus dem 1×1 zerlegt werden können.
Beispiele dafür sind:
- \(35 = 5\cdot 7 \)
- \(56 = 7\cdot 8 = 7 \cdot 2 \cdot 2 \cdot 2 \)
- \(63 = 7\cdot 9 = 7 \cdot 3 \cdot 3 \)
Wenn du alle Zahlen aus dem 1×1 markierst, siehst du in der 100er Tabelle oder Hundertertafel viele Zahlen, die nicht dazu gehören. Aber nicht alle Zahlen, die im kleinen Einmaleins nicht auftauchen sind Primzahlen. Alle anderen Zahlen davon sind Vielfache von kleineren Primzahlen, wie z.B.
- \(22 =2 \cdot 11 \)
- \(57 = 3\cdot 19 \)
- \(92 = 4\cdot 23 \)
57 kannst du aber auch als Zahl in der Fortsetzung der 3er Reihe sehen, nämlich an der 19. Stelle.
Liste aller Primzahlen bis 100:
2, 3, 5, 7, 11, 13, 17, 19,
23, 29, 31, 37,
41, 43, 47, 53, 59,
61, 67, 71, 73, 79,
83, 89, 97
Primzahlen - in der Hunderter Tabelle
Die Primzahlen kann man auch in der Hunderter Tabelle markieren.
Achte in der Zahlentabelle bis 100 auf die Farben!
- alle Zahlen aus dem 1×1 (ohne die Primzahlen bis 10: 2,3,7)
- Vielfache von Primzahlen
- die Primzahlen bis 100
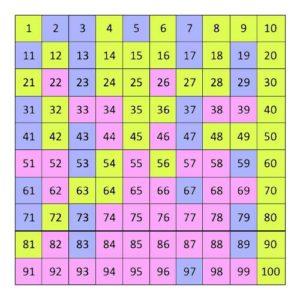
Alle Zahlen bis 100, farbig markiert.
Primzahlen in dieser Farbe!
Welche Zahlen sind Primzahlen - berechnen mit der Primfaktorzerlegung
Wie viele Primzahlen gibt es - probiere es aus mit der online Primzahlzerlegung
Primfaktorzerlegung online
Wir haben ein kleines Programm geschrieben, das Zahlen in Primfaktoren zerlegen kann. Probiere es aus. Die Eingabe prüft noch nicht, ob es sich um eine gültige Zahl handelt. Daher musst du darauf achten, dass wirklich nur Ziffern in das Feld eingegeben werden!
Primzahlen bis 100 - die Primfaktorzerlegung
Damit du die Primfaktorzerlegung besser verstehst haben wir hier alle Zahlen von 1 bis 100 in Primfaktoren zerlegt, sofern es möglich ist.
1 – 25 – die Primfaktorzerlegung
1 – 25
- \(1=1 \cdot 1 \) keine Primzahl
- \( 2 = 1\cdot 2 \) Primzahl
- \( 3 = 1\cdot 3 \) Primzahl
- Primfaktorzerlegung 4 \( = 2\cdot 2 =2^2\)
- \(5 = 1\cdot 5 \) Primzahl
- Primfaktorzerlegung 6 \( = 2\cdot 3 \)
- \(7 = 1\cdot 7 \) Primzahl
- Primfaktorzerlegung 8 \( = 2\cdot 2 \cdot 2=2^3\)
- Primfaktorzerlegung 9 \( = 3\cdot 3=3^2 \)
- Primfaktorzerlegung 10 \( = 2\cdot 5 \)
- \(11 = 1\cdot 11 \) Primzahl
- Primfaktorzerlegung 12 \( = 2\cdot 2 \cdot 3 \)
- \(13 = 1 \cdot 13 \) Primzahl
- Primfaktorzerlegung 14 \( = 2\cdot 7 \)
- Primfaktorzerlegung 15 \( = 3\cdot 5 \)
- Primfaktorzerlegung 16 \( = 2\cdot 2 \cdot 2 \cdot 2 =2^4\)
- \(17 = 1 \cdot 17\) Primzahl
- Primfaktorzerlegung 18 \( = 2\cdot 3 \cdot 3 \)
- \(19 = 1\cdot 19 \) Primzahl
- Primfaktorzerlegung 20 \( = 2\cdot 2 \cdot 5 \)
- Primfaktorzerlegung 21 \( = 3\cdot 7 \)
- Primfaktorzerlegung 22 \( = 2\cdot 11 \)
- \(23 = 1 \cdot 23 \) Primzahl
- Primfaktorzerlegung 24 \( = 2\cdot 2\cdot 2 \cdot 3 \)
- Primfaktorzerlegung 25 \( = 5\cdot 5=5^2 \)
Primfaktorzerlegung bis 50
26 – 50
- Primfaktorzerlegung 26 \(=2\cdot 13 \)
- Primfaktorzerlegung 27 \( = 3\cdot 3 \cdot 3 \)
- Primfaktorzerlegung 28 \( = 2\cdot 2 \cdot 7 \)
- \(29 = 1\cdot 29 \) Primzahl
- Primfaktorzerlegung 30 \( = 2\cdot 3 \cdot 5 \)
- \(31 = 1\cdot 31 \) Primzahl
- Primfaktorzerlegung 32 \( = 2\cdot 2 \cdot 2 \cdot 2 \cdot 2 =2^5\)
- Primfaktorzerlegung 33 \( = 3\cdot 11\)
- Primfaktorzerlegung 34 \( = 2\cdot 17 \)
- Primfaktorzerlegung 35 \( = 5\cdot 7 \)
- Primfaktorzerlegung 36 \( = 6\cdot 6=6^2 \)
- \(37= 1\cdot 37\) Primzahl
- Primfaktorzerlegung 38\( = 2 \cdot 19 \)
- Primfaktorzerlegung 39 \( = 3\cdot 13 \)
- Primfaktorzerlegung 40 \( = 2\cdot 2 \cdot 2 \cdot 5\)
- \(41 = 1\cdot 41 \) Primzahl
- Primfaktorzerlegung 42 \(= 2 \cdot 3 \cdot 7\)
- \(43 = 1\cdot 43 \) Primzahl
- Primfaktorzerlegung 44 \( = 2\cdot 2 \cdot 11\)
- Primfaktorzerlegung 45 \( = 3\cdot 3 \cdot 9 \)
- Primfaktorzerlegung 46 \( = 2\cdot 23 \)
- \(47 = 1\cdot 47 \) Primzahl
- Primfaktorzerlegung 48 \( = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \)
- Primfaktorzerlegung 49 \( = 7\cdot 7=7^2 \)
- Primfaktorzerlegung 50 \( = 2\cdot 5\cdot 5 \)
Die Primfaktorzerlegung bis 75
51 – 75
- \(51 = 3\cdot 17 \)
- \(52 = 2\cdot 2 \cdot 13 \)
- \(53 = 1\cdot 53 \) Primzahl
- \(54 = 2\cdot 3 \cdot 3 \cdot 3 \)
- \(55 = 5\cdot 11 \)
- \(56 = 2\cdot 2 \cdot 2 \cdot 7 \)
- \(57 = 3\cdot 19 \)
- \(58 = 2\cdot 29 \)
- \(59 = 1\cdot 59 \) Primzahl
- \(60 = 2\cdot 2 \cdot 3 \cdot 5 \)
- \(61 = 1\cdot 61 \) Primzahl
- \(62 = 2\cdot 31 \)
- \(63 = 3 \cdot 3 \cdot 7 \)
- \(64=2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 =2^6\)
- \(65 = 5\cdot 13 \)
- \(66 = 2\cdot 3 \cdot 11\)
- \(67 = 1\cdot 67 \) Primzahl
- \(68 = 2\cdot 2 \cdot 17 \)
- \(69 = 3\cdot 23 \)
- \(70 = 2\cdot 5 \cdot 7 \)
- \(71 = 1\cdot 71 \) Primzahl
- \(72 = 2\cdot 2 \cdot 2 \cdot 3 \cdot 3 \)
- \(73 = 1\cdot 73 \) Primzahl
- \(74 = 2\cdot 37\)
- \(75 = 3\cdot 5 \cdot 5 \)
76 bis 100 Primfaktorzerlegung
76 – 100
- \(76 = 2\cdot 2 \cdot 19 \)
- \(77 = 7\cdot 11\)
- \(78 = 2\cdot 3 \cdot 13 \)
- \(79 = 1\cdot 79\) Primzahl
- \(80 = 2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 5 \)
- \(81 = 3\cdot 3 \cdot 3 \cdot 3=3^4\)
- \(82 = 2\cdot 41 \)
- \(83 = 1\cdot 83 \) Primzahl
- \(84 = 2 \cdot 2\cdot 3 \cdot 7 \)
- \(85 = 5 \cdot 17 \)
- \(86= 2 \cdot 43 \)
- \(87 = 3 \cdot 29 \)
- \(88 = 2 \cdot 2\cdot 2 \cdot 11 \)
- \(89 = 1 \cdot 89 \) Primzahl
- \(90 = 2 \cdot 3\cdot 3 \cdot 5 \)
- \(91 = 7 \cdot 13 \)
- \(92 = 2 \cdot 2\cdot 23 \)
- \(93 = 3 \cdot 31 \)
- \(94 = 2 \cdot 47 \)
- \(95 = 5 \cdot 19 \)
- \(96 = 2 \cdot 2\cdot 2 \cdot 2 \cdot 2 \cdot 3 \)
- \(97 = 1 \cdot 97 \) Primzahl
- \(98 = 2 \cdot 7\cdot 7 \)
- \(99 = 3 \cdot 3\cdot 11 \)
- \(100 = 2 \cdot 2\cdot 5 \cdot 5 \)
Primzahlen - So erkennst du sie mit den Teilbarkeitsregeln
Primfaktorzerlegung von Hand – durch Kopfrechnen und Regeln zur Teilbarkeit
Willst du selbst ohne Computer eine Zahl in Faktoren zerlegen, musst du einige Teilbarkeitsregeln kennen.
Die wichtigsten listen wir hier auf:
Teilbarkeit durch 2
- Die einfachste kennst du seit der Grundschule: Jede gerade Zahl ist durch 2 teilbar!
Teilbarkeit durch 3
- Ist die Quersumme einer Zahl durch 3 teilbar, so ist die Zahl durch 3 teilbar!
Teilbarkeit durch 4
- Ist eine Zahl zweimal durch 2 teilbar oder eine Zahl geteilt durch 2 immer noch gerade, dann ist sie durch 4 teilbar.
- Alternativ gilt auch: ist die Zahl, die von den letzten 2 Stellen gebildet wird (Einer und Zehner), durch 4 teilbar, dann ist die Zahl durch 4 teilbar. Es gilt nämlich dann, dass die weiteren Stellen ab der 3. Stelle Hunderter sind. Denn alle Hunderter sind durch 4 teilbar (\( 100 = 4 \cdot 25 \)).
Teilbarkeit durch 5
- Eine Zahl ist durch 5 teilbar, wenn die letzte Ziffer eine 5 oder 0 ist.
Teilbarkeit durch 6
- Eine gerade Zahl, deren Quersumme durch 3 teilbar ist, ist durch 6 teilbar.
- Die obige Regel beinhaltet die Regeln zur Teilbarkeit durch 2 und durch 3.
Teilbarkeit durch 9
- Eine Zahl ist durch 9 teilbar, wenn die Quersumme durch 9 teilbar ist.
Primzahl Kreuzworträtsel
Ein Primzahl Kreuzworträtsel ist hier in Vorbereitung!
