Flächeninhalt Rechteck berechnen - interaktive Aufgaben Rechteck
Flächeninhalt Rechteck
Flächeninhalt Rechteck meistern
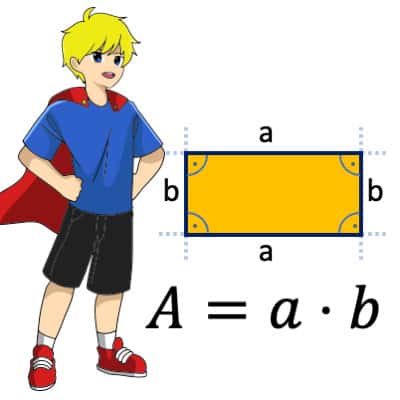
Um den Flächeninhalt eines Rechtecks zu berechnen betrachten wir zunächst einmal ein Rechteck.
Das Rechteck
Ein Rechteck ist eine geometrische Figur, die aus vier Seiten besteht. Es ist eine spezielle Art von Viereck, bei dem alle Innenwinkel 90 Grad betragen. Das bedeutet, dass die Seiten, die aufeinanderstoßen, einen rechten Winkel (90 Grad) bilden. Gegenüberliegende Seiten sind beim Rechteck gleich lang.
Ebenso heißt das, dass ein Rechteck zwei Paare von parallelen Seiten hat, die jeweils gleich lang sind, während die anderen beiden Seiten auch gleich lang sind.
Die Länge der längeren Seite eines Rechtecks wird oft als „Länge“ bezeichnet, während die Länge der kürzeren Seite oft als „Breite“ bezeichnet wird.
Die Eigenschaften des Rechtecks machen es zu einer nützlichen geometrischen Form in vielen praktischen Anwendungen, einschließlich Bauwesen, Handel, Landwirtschaft, Vermessung und Geometrie.
Weitere Infos zum Rechteck findest du zum Beispiel bei Wikipedia: https://de.wikipedia.org/wiki/Rechteck
Flächeninhalt Rechteck berechnen
Wir berechnen den Flächeninhalt eines Rechtecks, indem wir einfach die Länge (auch als „Seitenlänge“ oder „Seitenmaß“ bezeichnet, wir nehmen den Buchstaben a) mit der Breite (ebenfalls als „Seitenlänge“ oder „Seitenmaß“ bezeichnet, wie nehmen den Buchstaben b) multiplizieren.
Flächeninhalt Rechteck Formel
Die Formel für den Flächeninhalt eines Rechtecks lautet :
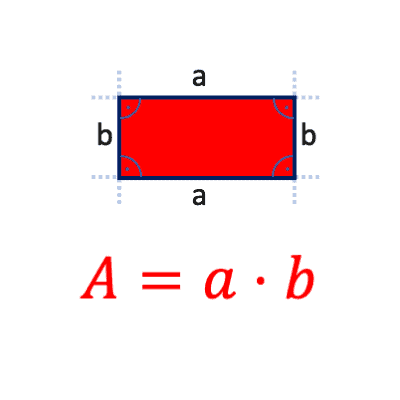
Flächeninhalt = \(Länge \cdot Breite = a \cdot b \)
Manchmal wird auch die Abkürzung „A“ für den Flächeninhalt verwendet. In diesem Fall lautet die Formel:
\( A = a \cdot b \) oder \( A = l \cdot b \)
Zum Beispiel hat ein Rechteck mit einer Länge von 5 cm und einer Breite von 3 cm einen Flächeninhalt von:
Flächeninhalt = \( 5 cm \cdot 3 cm = 15 cm^2 \)
Die Fläche des Rechtecks in unserem Beispiel beträgt 15 Quadratzentimeter.
Wichtig bei der Flächenberechnung mit Längen ist es, dass jede Länge eine Längeneinheit hat, wie zum Beispiel cm (Zentimeter). Dann ergibt sich als Flächeneinheit die Einheit cm x cm = cm^2 = Quadratzentimeter
Flächeninhalt Rechteck Rechner
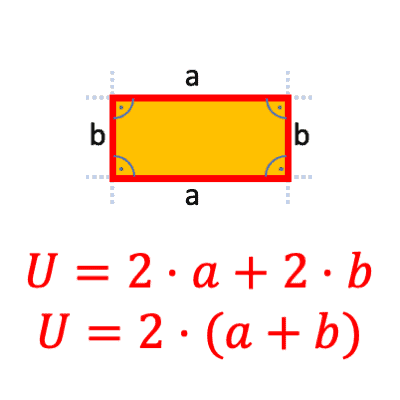
Umfang Rechteck berechnen
Wie berechnet man den Umfang eines Rechtecks
Der Umfang eines Rechtecks ist die Länge der Grenzlinie, die alle vier Seiten des Rechtecks umgibt. Um den Umfang eines Rechtecks zu berechnen, addiert man einfach die Längen aller vier Seiten zusammen.
Umfang Rechteck Formel
Die Formel für den Umfang eines Rechtecks lautet:
Umfang = \( 2 \cdot a + 2 \cdot b = 2 \cdot (a + b) \)
wobei a = die Länge des Rechtecks und b die Breite des Rechtecks ist.
Zum Beispiel hat ein Rechteck mit einer Länge von a = 8 cm und einer Breite von b = 5 cm einen Umfang von:
Umfang \( = 2 \cdot (8 cm + 5 cm) = 2 \cdot 13 cm = 26 cm \)
Der Umfang des Rechtecks beträgt U = 26 cm (Zentimeter).
Umfang Rechteck Rechner
Rechteck Aufgaben interaktiv
Interaktive Aufgaben zum Flächeninhalt eines Rechtecks
Rechteck und Quadrat das Infoposter als PDF
Infoposter
Quadrat & Rechteck
Deutsch
Infoposter
Quadrat & Rechteck
Englisch
Infoposter
Quadrat & Rechteck
Spanisch
Infoposter
Quadrat & Rechteck
Französisch
Merkhilfe - Quadrat und Rechteck
Merkblatt zu Quadrat und Rechteck
Definitionen:
- Ein Quadrat ist ein spezielles Rechteck, bei dem alle vier Seiten gleich lang sind.
- Das Rechteck ist eine geometrische Form mit vier Seiten und vier Winkeln, wobei gegenüberliegende Seiten gleich lang sind und alle Winkel 90 Grad messen.
Eigenschaften:
- Quadrat: Gleichlange Seiten, gleichgroße Winkel, diagonale Länge = Seitenlänge * Wurzel aus 2
- Rechteck: Gegenüberliegende Seiten sind gleich lang, gegenüberliegende Winkel sind gleich groß, diagonale Länge = Wurzel aus (Seitenlänge^2 + Seitenbreite^2)
Formeln:
- Fläche des Quadrats: Seitenlänge^2
- Umfang des Quadrats: 4 * Seitenlänge
- Fläche des Rechtecks: Seitenlänge * Seitenbreite
- Umfang des Rechtecks: 2 * (Seitenlänge + Seitenbreite)
Beispiele:
- Ein klassisches Schachbrett hat 64 Felder, die alle quadratisch sind.
- Ein Fenster kann als Rechteck modelliert werden, um seine Abmessungen und Größe zu berechnen.
Übungen:
- Berechne die Fläche und den Umfang eines Quadrats mit einer Seitenlänge von 5 cm.
- Berechne die Fläche und den Umfang eines Rechtecks mit einer Seitenlänge von 6 cm und einer Seitenbreite von 4 cm.
- Zeichne ein Rechteck mit einer Fläche von 20 cm² und bestimme seine Abmessungen.
Merkhilfen:
- Ein Quadrat hat 4 gleich lange Seiten.
- Diagonalen von Quadraten und Rechtecken können berechnet werden, indem man die Seitenlängen in eine Formel einsetzt.
- Die Formel für den Umfang eines Rechtecks lautet: 2 * (Seitenlänge + Seitenbreite).
Anwendungen:
- Architekten verwenden Quadrat- und Rechtecksformen bei der Planung von Gebäuden.
- Designer verwenden diese Formen bei der Gestaltung von Möbeln und anderen Objekten.
- In der Geometrie sind Quadrat- und Rechtecksformen ein wichtiger Bestandteil bei der Untersuchung von Formen und Flächen.
Zusammenfassung:
- Quadrat: Alle Seiten sind gleich lang, Fläche = Seitenlänge^2, Umfang = 4 * Seitenlänge
- Rechteck: Gegenüberliegende Seiten sind gleich lang, Fläche = Seitenlänge * Seitenbreite, Umfang = 2 * (Seitenlänge + Seitenbreite)
- Diagonalen können berechnet werden, indem man die Seitenlängen in eine Formel einsetzt.
- Quadrat- und Rechtecksformen haben Anwendungen in Architektur, Design und Geometrie.
Die wichtigsten Infos zu Quadrat und Rechteck haben wir auf unserem Infoposter zusammengestellt!
Flächenberechnung von Rechtecken – Wo braucht man das?
Die Berechnung des Flächeninhalts von Rechtecken wird in vielen Bereichen der Praxis verwendet. Hier sind nur einige Beispiele:
- Bauwesen: Beim Bau von Gebäuden oder Strukturen müssen Architekten und Ingenieure den Flächeninhalt von Rechtecken berechnen, um die Menge an Materialien wie Holz, Beton, Fliesen oder Farbe zu bestimmen, die für den Bau benötigt wird.
- Handel: Im Handel wird die Berechnung des Flächeninhalts von Rechtecken verwendet, um den Preis von Produkten zu bestimmen, die auf der Basis ihrer Größe oder Abdeckung verkauft werden. Beispiele hierfür sind Teppiche, Bodenbeläge und Wandfliesen.
- Landwirtschaft: Bei der Planung und Verwaltung von landwirtschaftlichen Flächen muss die Größe von Feldern, Weiden und Anbauflächen berechnet werden, um die Menge an Saatgut, Düngemitteln und Pestiziden zu bestimmen, die benötigt werden.
- Vermessung: Vermesser verwenden die Flächenberechnung von Rechtecken, um Landgrenzen zu vermessen, die Grundstücksgröße zu bestimmen oder die Fläche von Gebäuden oder anderen Strukturen zu ermitteln.
- Geometrie: Die Berechnung des Flächeninhalts von Rechtecken ist auch in der Geometrie von Bedeutung, da sie eine wichtige Grundlage für die Berechnung von Flächen anderer Formen wie Dreiecke, Trapeze und Kreise bildet.
Diese Beispiele zeigen, wie wichtig die Berechnung des Flächeninhalts von Rechtecken in vielen Bereichen der Praxis ist.