Geometrie Grundbegriffe - online Geometrie lernen
Geometrie Werkzeuge - was wir dafür brauchen

Lerne die Geometrie Grundbegriffe auf dieser Seite kennen.
Bevor wir richtig loslegen, benötigen wir einige Hilfsmittel oder Werkzeuge für unsere Arbeit:
- Bleistift (und ein Bleistiftspitzer)
- Radiergummi
- Lineal
- Geodreieck / Winkelmesser
- Zirkel
- ein Rechenheft mit karierten Seiten
Achte darauf, dass der Bleistift immer gespitzt ist. Zeichne sauber in dein Heft.
Auch wenn wir immer öfter mit einem PC oder Tablet Computer digital arbeiten ist es wichtig, Geometrie mit Zirkel und Lineal ganz klassisch auf Papier zu lernen. Außerdem macht es viel mehr Spass, selbst auf Papier zu zeichnen!
Koordinatensystem
Was ist ein Koordinatensystem?
Ein Koordinatensystem ist für uns das Bezugssystem zum Zeichnen von Punkten und anderen geometrischen Objekten.
Was ist das Koordinatensystem in Zeiten von GPS, Mobiltelefon und Navigationssystemen?
Ohne ein Koordinatensystem oder ein Bezugssystem könnten wir uns im 2-dimensionalen oder auch 3-dimensionalen Raum nicht bewegen und Ziele finden. Nur wenn für jeden der gleiche Bezugspunkt vorhanden ist, ist die Lage eines Punktes eindeutig.
In der realen Welt in der Zeit von Navigationssystemen, mobilen Geräten und geografischen Karten wird das Koordinatensystem von den GPS-Koordinaten und damit durch die Längen und Breitengrade der Erdkugel bestimmt.
Ein Koordinatensystem für unsere Arbeit besteht aus:
- 2 Achsen, der waagrechten x-Achse (1) und der senkrechten y-Achse (2). Beide Achsen stehen immer aufeinander senkrecht!
- dem Ursprung oder auch Nullpunkt (3), das ist der Schnittpunkt der x-Achse und der y-Achse.
- einer Skalenteilung auf der x- Achse (4) und der y-Achse (5). Diese Skalenteilung wird normalerweise im Heft alle 2 Kästchen oder im Abstand von 1 cm eingezeichnet!
Merke:
An das rechte Ende der x-Achse sowie an das obere Ende der y-Achse zeichnen wir einen kleinen Pfeil und beschriften die Achse mit x bzw. y. Betrachte hierzu das abgebildete Koordinatensystem.
Punkte im Koodinatensystem / die Koordinaten eines Punktes
Punkte geben einen genauen Ort in einem Koordinatensystem an, ähnlich wie auf einer Landkarte.
Jeder Punkt wird mit einem großen Buchstaben angegeben / gekennzeichnet!
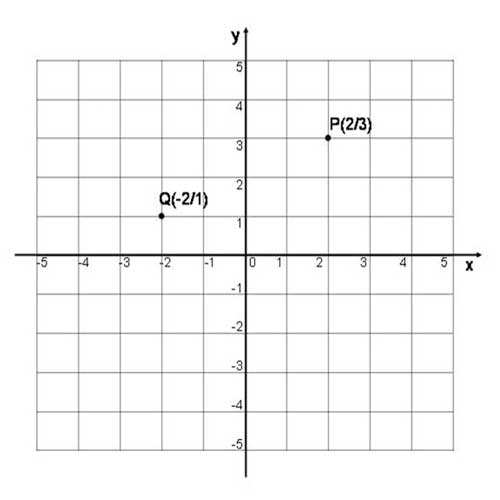
In dem Koordinatensystem unten sind dies die Punkte P und Q.
Jeder Punkt ist eindeutig durch eine x-Koordinate und eine y-Koordinate bestimmt.
P (2 | 3) bedeutet:
Gehe auf der x-Achse 2 Schritte in positiver Richtung (nach rechts) und dann 3 Schritte senkrecht hierzu in die positive y-Richtung (nach oben).
Q (-2 | 1) bedeutet:
Gehe auf der x-Achse 2 Schritte in negativer Richtung (nach links) und dann 1 Schritt senkrecht hierzu in positive y-Richtung (nach oben).
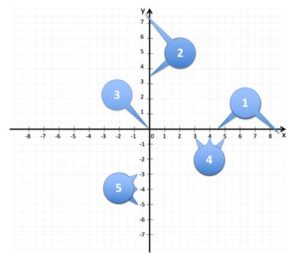
Beispiel und erste online Übung: Punkte im Koordinatensystem
Bestimme die Koordinaten der folgenden Punkte
P, Q, R, S, T, U im Koordinatensystem.
Trage die x-Koordinate und y-Koordinate aller Punkte in die Felder ein!
Strecke im Koordinatensystem
Was ist eine Strecke in der Geometrie?
Eine gerade Linie zwischen zwei Punkten heißt Strecke.
Die Strecke im Koordinatensystem ist einer der Geometrie Grundbegriffe, die du perfekt kennen musst!
Eine Strecke wird mit einem kleinen Buchstaben gekennzeichnet. Nehmen wir als Beispiel die Strecke s zwischen den Punkten P und Q:
\( s=\overline{PQ} \)
Wir verstehen den Begriff “Strecke” besser mit einer Aufgabe als Beispiel.
- Wir zeichnen in ein Koordinatensystem die Punkte P (2 | 1) und Q (4 | 3).
- Jetzt verbinden wir die Punkte P und Q.
Wir erhalten die Strecke \( s=\overline{PQ} \)
Starte das kleine Video, dann siehst du, wie die Aufgabe gelöst wird!
Merke:
Eine Strecke kennzeichnen wir, indem wir Anfangs- und Endpunkt (in Großbuchstaben) zusammenschreiben und mit einem Strich über den beiden Buchstaben versehen!
Die Länge einer Strecke \( s=\overline{PQ} \) heißt auch Entfernung oder Abstand der Punkte P und Q.
Sie wird mit \( |s|=|\overline{PQ}| \) bezeichnet.
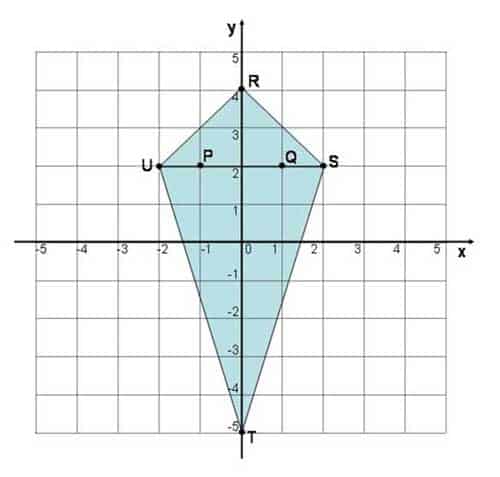
Online Übung Strecke im Koordinatensystem
Betrachte die gezeichneten Strecken und die Punkte, die rechts angegeben sind.
Ziehe die richtigen Bezeichnungen für die Strecken an die richtige Stelle in das Schaubild!
Du kannst die Aufgabe auf dem Bildschirm maximieren!
Gerade im Koordinatensystem
Was ist eine Gerade?
Eine Gerade ist eine gerade Linie ohne einen Anfangs- und Endpunkt. Geraden werden mit kleinen Buchstaben bezeichnet.
Obwohl eine Gerade unendlich lang ist können wir eine Gerade immer nur mit einer bestimmten Länge einzeichnen, da der Platz im gezeichneten Koordinatensystem begrenzt ist.
Merke:
Durch zwei verschiedene Punkte gibt es immer nur genau eine Gerade!
Wir wollen die Gerade besser kennen lernen und machen dazu eine kleine Übung.
Übung:
Zeichne die Punkte P (-2 | -2) und Q (3 | 3) in das nebenstehende Koordinatensystem und zeichne die Gerade g, die durch beide Punkte verläuft.
Bestimme jetzt den Schnittpunkt S der Geraden g mit der bereits eingezeichneten Geraden h.
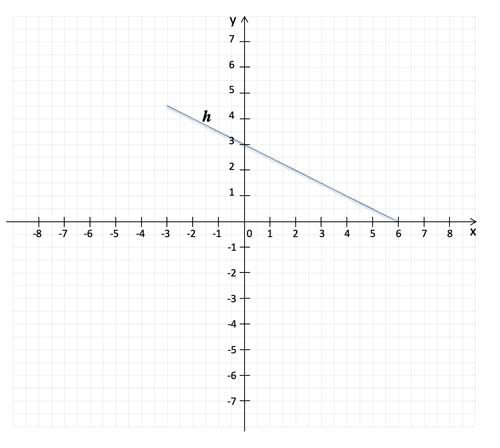
Unten in dem kleinen Video zeigen wir dir die Lösung!
Online Übung Gerade im Koordinatensystem
Die Übung:
Gegeben sind die folgenden Geraden im Bild nebenan:
- g verläuft durch die Punkte A und B.
- h verläuft durch die Punkte C und D.
- l verläuft durch die Punkte E und F.
- m verläuft durch die Punkte G und H.
Ziehe die Namen der Geraden an die richtige Stelle!
Die Übungshefte für Klasse 2
Diese Übungshefte haben nicht viel mit Winkel messen oder Winkel zeichnen zu tun. Aber sie enthalten viele interaktive Übungen von dieser WEB-Seite!



