Prozente berechnen - Brüche + Dezimalbrüche in Prozent umwandeln
Prozente berechnen

wie man mit Prozenten rechnet.
Prozente berechnen – Wir rechnen mit Prozenten, Brüchen und Dezimalbrüchen?
Das Prozentzeichen: %
Prozent heißt “von Hundert”. Das bedeutet 10 % sind 10 von hundert Teilen. Damit hat man eine gleiche Beschreibung für Anteile wie bei Brüchen und Dezimalbrüchen. Hier lernen wir, wie man Brüche in Prozente umrechnet oder Prozent berechnen kann, wenn man den Bruch oder den Dezimalbruch kennt.

20% des Gitters (20 von 100 Kästchen)
30 % des Gitters (30 von 100 Kästchen)
50 % des Gitters (50 von 100 Kästchen)
100 % = das gesamte Gitter (100 Kästchen)
Merke dir einfach: Prozente sind Hundertstel!
- 1 % = 1 Teil von 100 = \( \frac {1}{100}=0,01 \)
- 10 % = 10 Teile von 100 = \( \frac {10}{100} = \frac {1}{10}=0,1\)
- 50 % = 50 Teile von 100 = \( \frac {50}{100} =\frac {1}{2}=0,5 \)
Übrigens: Tausendstel nennt man “Promille” (von tausend).
Um einen Bruchteil in Prozent umzuwandeln müssen wir den Bruch erweitern oder kürzen, damit im Nenner des Bruchs die Zahl 100 steht. Der Zähler gibt dann den Prozentanteil an!

Vorübung zum Start: Hast du die Umwandlung verstanden?
Ziehe die richtigen Zahlen an die dafür vorgesehenen Stellen!
online Übungen | Prozente - Brüche - Dezimalbrüche
Übung 2 (A) – einfache Prozente | Wandle die Dezimalzahlen in Prozente um!
Übung 2 (B) – einfache Prozente | Wandle die Brüche in Prozente um!
Wir wandeln Brüche in Prozente um
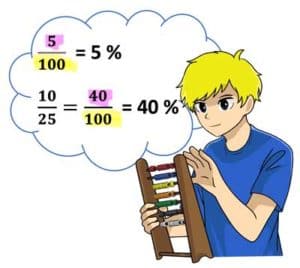
im Nenner des Bruchs muss 100 stehen!
So kannst du Brüche in Prozent umwandeln
Alle Brüche mit einer Zehnerpotenz (Zehnerzahl 10, 100, 1000, …) im Nenner können als Dezimalbruch oder Dezimalzahl geschrieben werden und damit auch als Prozentzahl!
Beispiele:
(1) \(\frac{43}{100} =43 \% \) somit sind 43 Hundertstel = 43 %
(2) \(\frac{124}{1000} =12,4 \% \) , somit sind 124 Tausendstel = 12,4 Hundertstel = 12,4 %
Steht im Nenner noch keine Zehnerzahl (Zehnerpotenz), gilt die folgende Regel:
Kannst du den Nenner eines Bruchs durch Kürzen oder Erweitern auf 100 bringen, dann kann man den Bruch auch als Prozent schreiben.
einige Beispiele:
(1) \(\frac{3}{5} = \frac{60}{100} =60 \% \)
(2) \(\frac{1}{4} = \frac{25}{100} = 25 \% \)

einfach ausdrucken oder
digital ausfüllen!
Arbeitsblätter Prozente berechnen
Die Aufgaben von dieser Seite als PDF zum Ausdrucken:
Gemischte Aufgaben
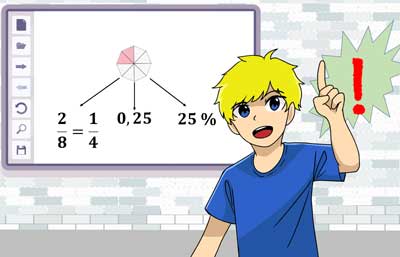
können den die gleiche Zahl darstellen!
Brüche, Dezimalzahlen und Prozente können die gleiche Zahl darstellen!
Siehe im Beispiel:
\(\frac{1}{4} = \frac{25}{100}=0,25 = 25 \% \)Diesen Zusammenhang vertiefen wir in der nächsten online Übung!
Übung 4 – Ergänze die fehlenden Brüche | Dezimalbrüche | Prozente
Übung 5 Prozente
Ziehe nur das zutreffende “Richtig” oder “Falsch” an die richtige Stelle!
Übung 6 Prozente
Ziehe nur das zutreffende “Richtig” oder “Falsch” an die richtige Stelle!
Übung 8 – Prozente | Kleideretiketten
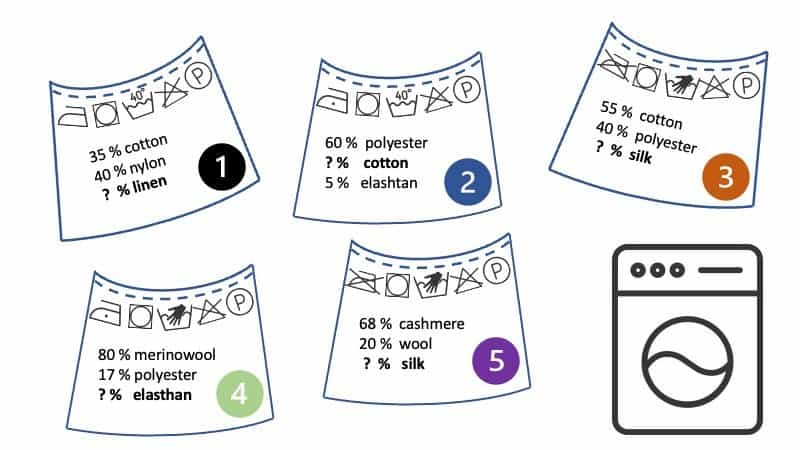
An verschiedenen Kleidungsstücken findest du die Zusammensetzung des Stoffes. Es gibt nur die angegebenen Materialien (zusammen also 100 %!) Bei jedem Etikett fehlt eine Prozentangabe. Berechne die fehlende Prozentangabe.
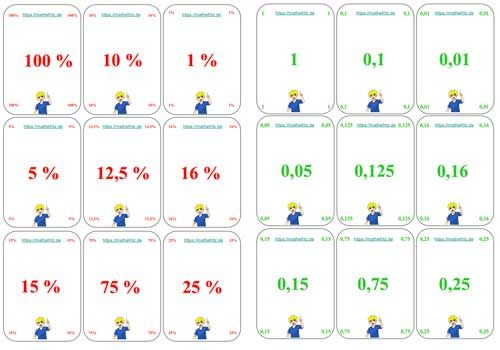
Mau-Mau Kartenspiel Bruchrechnung: Bruchteile, Prozente, Dezimalbrüche
Wir haben bereits gelernt, dass man einen Anteil als Bruch, als Dezimalzahl oder als Prozent schreiben kann.
Gleiche Werte gehören zusammen:
- Bruchteile als Anteile
- Brüche mit Zähler und Nenner
- Die Zahl als Dezimalbruch geschrieben
- Die Zahl als Prozentwert geschrieben
Wie in den hier gezeigten Beispielen: 1 Zehntel = \( \frac{1}{10} \) = 0,1 = 10 %
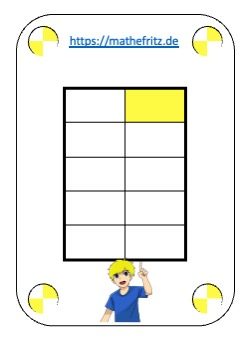
Anteil 1 von 10
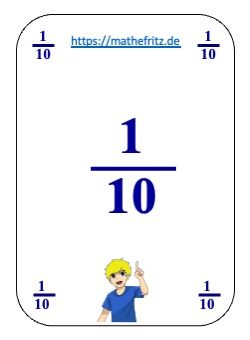
Bruch 1/10

Dezimalbruch 0,1

Prozentwert 10 %

zum Ausdrucken und basteln.
 Die Spielkarten / Lernkarten zur Bruchrechnung könnt ihr hier kostenlos ausdrucken!
Die Spielkarten / Lernkarten zur Bruchrechnung könnt ihr hier kostenlos ausdrucken!
Spielkarten Bruchrechnen lernen (PDF) 4 Seiten
Wenn Euch die Karten gefallen wäre es nett, wenn Ihr einen Link zu dieser Seite setzt oder die Seite bei Facebook / Instagram teilt!
Spielanleitung für das Mau-Mau Kartenspiel Bruchrechnung lernen:
Bruchteile – Brüche – Prozente- Dezimalbrüche
Spiele das Kartenspiel als Mau-Mau, Mau-Mau (für 2 bis 4 Spieler):
- Mische die Karten
- Jeder Spieler erhält 6 Karten. Bei mehr als 4 Spielern entsprechend weniger.
- Eine Karte vom verbleibenden Stapel wird aufgedeckt, der restliche Stapel bleibt umgedreht daneben liegen.
- Der jüngste Spieler beginnt.
- Die Karten dürfen dann aufeinander gelegt werden, wenn sie die gleiche Farbe haben oder das Deckblatt den gleichen Wert anzeigt, z.B. ½ = 50 % = 0,5 !
- Wenn keine Karte gelegt werden kann, muss eine neue Karte vom Stapel gezogen werden.
- Eine Besonderheit ist der Joker: Die Karten mit dem Wert 1 gelten als Joker. Sie können immer eingesetzt werden. Der Spieler, der diese Karte, den Joker einsetzt, darf den Wert und die Farbe der aktuellen Karte neu bestimmen.
Spiele das Spiel als Quartett (mit 2 bis 4 Spielern) :
- Alle Karten werden zwischen den Spielern aufgeteilt. Es gilt, Quartette, das heißt immer 4 Karten zu sammeln, die gleichen Wert haben.
- Abwechselnd werden Karten vom Nebenmann gezogen.
- Vollständige Quartette werden abgelegt.
- Es gewinnt die Person, die am Ende die meisten vollständigen Quartette gesammelt hat.
Bastelanleitung für die Spielkarten – Die Karten selbst basteln
- Drucke die 4 Seiten mit den Karten auf Karton oder dickes Papier.
- Tipp: Wenn die Seiten fertig ausgedruckt, laminiere sie und schneide sie erst dann aus! Das ergibt die beste Qualität.
Das Buch mit vielen Aufgaben zur Bruchrechnung: "Mathestunde 5 - Einfache Bruchteile"
Das Übungsheft zum Einstieg in die Bruchrechnung, mit vielen Dezimalbrüche Aufgaben in einem Heft!
Mathestunde 5 – Einfache Bruchrechnung
Übungsheft für die 5. Klasse / 6. Klasse
- Umfang: 60 Seiten, DIN A 4, geheftet, s/w
- Erschienen: 2015
- ISBN: 978-394186817-5
- Preis: 5,95 €
- Überall erhältlich in jeder Buchhandlung (bestellbar) oder in online Shops.