Réduire et étendre les fractions - Feuilles de calcul en ligne
Raccourcissement et allongement des fractions expliqués simplement
Qu'entend-on par raccourcissement et allongement des fractions ?
Nous commençons par un exercice pour vous mettre sur la voie !
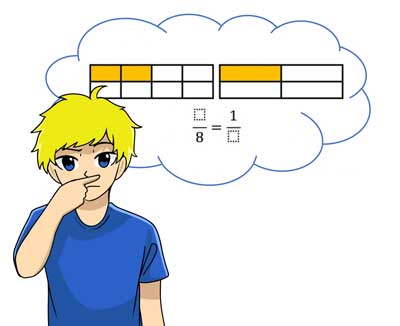
Dans l'image ci-contre, nous avons divisé un rectangle une fois en 8 parties et une fois seulement en 4 parties. A chaque fois, cependant, la même zone est colorée en jaune. Combien de fractions y a-t-il dans chaque cas ?
Complétez le problème de la fraction sous l'image !
Résolvez les tâches interactives suivantes. Vous comprendrez alors mieux que deux fractions différentes peuvent avoir la même valeur. Nous allons maintenant examiner cette transformation plus en détail. On parle également de troncature et d'expansion des fractions.
Exercice 1
Additionnez les fractions de manière à ce qu'elles décrivent précisément les images ci-dessus !
Pour ce faire, faites glisser les numéros correspondants dans les espaces prévus à cet effet !
Prolonger les fractions
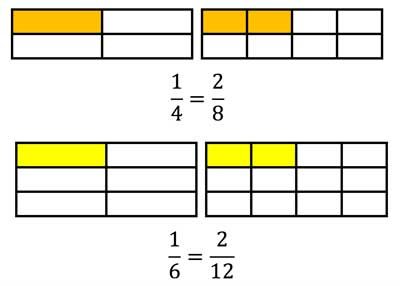
Dans l'image ci-dessus, nous apprenons à étendre les fractions avec 2
(Chaque fraction est divisée par deux dans le processus !)
Le numérateur et le dénominateur sont chacun multipliés par 2 !
\(\frac{1}{4}=\frac{1\cdot 2}{4\cdot 2}=\frac{2}{8} \)
\(\frac{1}{6}=\frac{1\cdot 2}{6\cdot 2}=\frac{2}{12} \)
Définition - Extension des fractions
L'extension d' une fraction signifie que nous multiplionsle numérateur et le dénominateur de la fraction par le même nombre.
Entermes visuels, l'extension signifie que nous continuons à diviser les fractions de la même manière.
Expansion de fractions Exemples :
\(\frac{1}{3}=\frac{1\cdot 2}{3\cdot 2}=\frac{2}{6}=\frac{2\cdot 3}{6\cdot 3}=\frac{6}{18}\)
\(\frac{3}{8}=\frac{3\cdot 2}{8\cdot 2}=\frac{6}{16}=\frac{6\cdot 3}{16\cdot 3}=\frac{18}{48}\)
\(\frac{2}{5}=\frac{2\cdot 2}{5\cdot 2}=\frac{4}{10}=\frac{4\cdot 3}{10\cdot 3}=\frac{12}{30}\)
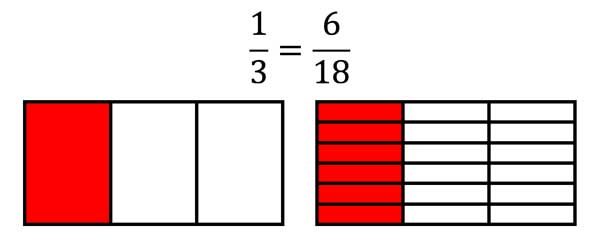
Ici, chaque pièce est à nouveau divisée en 6 parties.
Cela signifie qu'il faut s'étendre avec 6 !
Raccourcir les fractions
Définition - Réduction des fractions
Raccourcir une fraction signifie que nous divisons le numérateur et le dénominateur de la fraction par le même nombre.
RAPPEL !
Si l'on ne peut plus diviser le numérateur et le dénominateur d'une fraction par un nombre égal, on parle de fraction complètement tronquée.
Pour pouvoir diviser le numérateur et le dénominateur d'une fraction par le même nombre, nous devons vérifier très soigneusement par quels nombres le numérateur et le dénominateur sont divisibles. Pour ce faire, nous devons utiliser l'option Être capable d'appliquer les règles de divisibilité et la factorisation des nombres premiers !
Raccourcir les fractions Exemples :
\(\frac{6}{18}=\frac{6:3}{18:3}=\frac{2}{6} =\frac{2:2}{6:2}=\frac{1}{3} \)
\(\frac{42}{60}=\frac{42:6}{60:6}=\frac{7}{10} \)
\(\frac{48}{80}=\frac{48:8}{80:8}=\frac{6}{10} =\frac{6:2}{10:2}=\frac{3}{5} \)
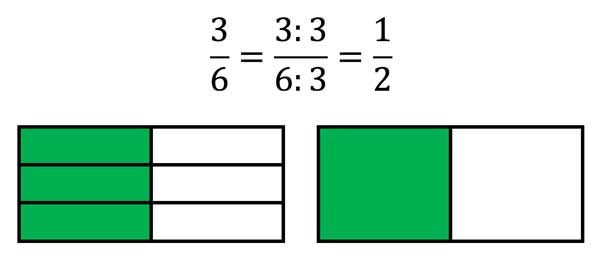
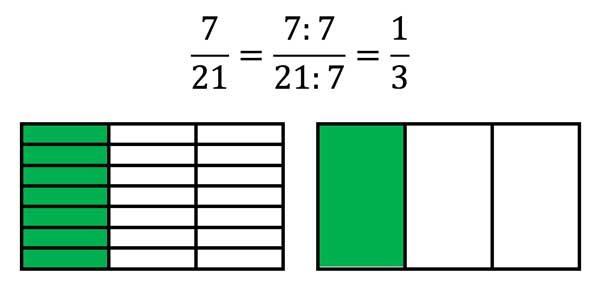
Dans les images ci-dessus, nous apprenons à raccourcir les fractions par 3 et par 7.
Toujours 3 ou toujours 7 pièces sont combinées en une seule pièce. Bien sûr, cela ne fonctionne que si le nombre total de toutes les parties est divisible par 3 ou par 7.
La décomposition en facteurs premiers pour réduire les fractions
La réduction des fractions devient particulièrement facile si nous divisons le numérateur et le dénominateur de la fraction en Décomposition des facteurs premiers. Nous pouvons alors simplement rayer les facteurs communs au numérateur et au dénominateur. On raccourcit complètement les fractions avec cette méthode!
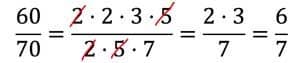
Si vous rencontrez toujours des problèmes avec la factorisation première, consultez notre page sur la divisibilité et la factorisation première et utilisez la fonction Calculatrice en ligne pour la factorisation des nombres premiers !
Avez-vous compris la méthode de raccourcissement complet avec la factorisation des nombres premiers ?
Faites le petit exercice en ligne pour le tester !
Procédez comme suit :
- Décomposez le numérateur et le dénominateur en facteurs premiers !
- Laissez les facteurs communs de côté !
- Saisissez à nouveau tous les facteurs restants !
- Notez toujours les chiffres dans l'ordre croissant (du plus petit au plus grand).
Réduire et étendre les fractions - exercices en ligne
Nous pratiquons l'expansion des fractions !
Notez la note sur le remplissage :
Entrez la valeur du numérateur pour A et la valeur du dénominateur pour B dans les champs vides. Malheureusement, l'outil en ligne de la tâche ne peut pas afficher cette entrée directement sur ou sous la ligne de fraction !
Exemple - Voici comment vous calculez les tâches dans l'exercice en ligne :
\( \frac{1}{2} \overset{ \cdot \text{10}}{=} \frac{A}{B}\) A = 10 B = 20\( \frac{12}{15} \underset{ \text{:3}}{=} \frac{A}{B}\) A = 4 B = 5Exercice 1 - Expansion de fractions
a) Développez toutes les fractions avec 3 !
b) Développez toutes les fractions avec 5 !
c) Développez toutes les fractions avec 8 !
Exercice 2 - Raccourcissement des fractions - simple
La brièveté ne concerne QUE le nombre indiqué sous le signe égal !
a) Raccourcissez la fraction dont le diviseur commun est le plus grand.
Dans cette tâche a), le diviseur commun est toujours sous le signe égal !
b) Raccourcir complètement pour que le numérateur et le dénominateur n'aient plus de diviseur commun !
Le résultat n'est correct que lorsqu'il est complètement raccourci !
c) Raccourcir complètement pour que le numérateur et le dénominateur n'aient plus de diviseur commun !
d) Raccourcir complètement pour que le numérateur et le dénominateur n'aient plus de diviseur commun !
Jeux de mémo : Trouver des fractions égales raccourcies ou étendues
Jeux de mémo - raccourcir et étendre les fractions
Trouvez les fractions ayant la même valeur ! Pour ce faire, vous devez étendre ou raccourcir une fraction pour trouver une fraction équivalente.
Mémo jeu 1
Le livre avec de nombreux exercices sur les fractions : "Cours de mathématiques 5 - Fractions simples".
Le cahier d'exercices pour débuter avec les fractions, de nombreuses tâches sur la réduction et l'extension des fractions dans un seul cahier !
Leçon de mathématiques 5 - Fractions simples
Cahier d'exercices pour les classes de 5e et 6e année
- Longueur : 60 pages, DIN A 4, cousu, n/b
- Publié : 2015
- ISBN : 978-394186817-5
- Prix : 5,95 €.
- Disponible partout dans toutes les librairies (à commander) ou dans les boutiques en ligne.

