Aufgaben Wahrscheinlichkeitsrechnung 🎲
Auf diese Seite findest du Aufgaben zur Wahrscheinlichkeitsrechnung, also Matheaufgaben Klasse 9. In der Regel sind diese Aufgaben Teil des Themas Wahrscheinlichkeitsrechnung in der Klasse 9 oder 10. Wir behandeln hier die Themen “bedingte Wahrscheinlichkeit”, “mehrstufige Wahrscheinlichkeit”, “Baumdiagramme”, “Ereignis und Ereignismenge” sowie “Aufgaben mit Glücksrädern” .
Wie funktioniert bedingte und mehrstufige Wahrscheinlichkeit? 🎲 🎱
Von mehrstufiger Wahrscheinlichkeit spricht man, wenn mehrere Zufallsexperimente nacheinander durchgeführt werden. Diese können die gleichen sein. Das können aber auch verschiedene sein. Um mehrstufige Zufallsexperimente besser zu verstehen ist es hilfreich, die Situation in einem Baumdiagramm darzustellen.
Beispiel: Wir werfen einen Würfel dreimal nacheinander. Das ist ein ganz einfaches mehrstufiges Zufallsexperiment.
Von bedingter Wahrscheinlichkeit spricht man, wenn bei einem Zufallsexperiment eine Bedingung vorgegeben wird. Beispiel siehe Aufgabe 3. Wenn bei der Aufgabenstellung die Bedingung ist, dass der Schüler aus der Mittelstufe ist. Löse die Aufgabe 3, um es besser zu verstehen.
Aufgaben zur Wahrscheinlichkeitsrechnung Blatt 1
Dieses Arbeitsblatt könnte eine Klassenarbeit mit einem Zeitaufwand von 45 Minuten sein. Dieser Aufwand gilt natürlich nur für die Bearbeitung auf einem Blatt Papier und nicht für die online Aufgaben auf dieser Seite.
Aufgabe 1:
Eine Urne enthält 4 weiße, 2 schwarze und 4 graue Kugeln.
Es werden zwei Kugeln nacheinander mit Zurücklegen gezogen (jede Kugel wird direkt wieder zurück gelegt).
- Zeichne den Ergebnisbaum und gib die Ergebnismenge an.
- Berechne die Wahrscheinlichkeit, zweimal hintereinander
eine weiße Kugel zu ziehen. - Berechne die Wahrscheinlichkeit, keine schwarze Kugel zu ziehen.
Nun wird eine Kugel unter der Bedingung B gezogen: die gezogene Kugel ist nicht weiß.
- Bestimme für jedes jetzt mögliche Ergebnis ω die Wahrscheinlichkeit P(ω) und PB(ω).
Das Modellbild zu der Aufgabe 1:
4 weiße Kugeln, 2 schwarze Kugeln, 4 graue Kugeln

Aufgabe 2:
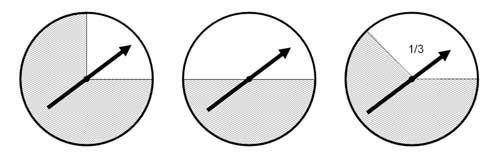
Die abgebildeten Glücksräder werden nacheinander gedreht.
Bei 1 € Einsatz erhält man folgenden Gewinn:
- 3 € bei zwei weißen Sektoren
- 5 € bei 3 weißen Sektoren.
- Modelliere das Zufallsereignis mit Hilfe eines Ergebnisbaums.
- Berechne die Wahrscheinlichkeit für einen Gewinn.
- Mache eine Gewinn- und Verlustrechnung für 1000 Versuche.
- Kann der Veranstalter mit dem Glücksspiel einen Gewinn machen oder Gewinnen die Spieler bei hoher Teilnehmerzahl mehr?
Aufgabe 3:
An der Schule befinden sich 1000 Schüler. 450 in der Unterstufe, 300 in der Mittelstufe und 250 in der Oberstufe. Bei einem Quiz nehmen 24 % der Unterstufenschüler, 15 % der
Mittelstufenschüler und 10 % der Oberstufenschüler teil.
Wie groß ist die Wahrscheinlichkeit, dass ein beliebiger teilnehmender Schüler aus der Mittelstufe den ersten Preis gewinnt?
Wie groß ist die Wahrscheinlichkeit, dass ein bestimmter teilnehmender Schüler aus der Mittelstufe einen neu eingeführten Mittelstufenpreis gewinnt?
Aufgabe 4:
Ein Jäger trifft bei einem Schuss mit 60 % Wahrscheinlichkeit ein Reh und mit 50 % Wahrscheinlichkeit ein Hasen. In der Nacht trifft er auf beide und kann jeweils nur einen Schuss abgeben.
- Wie hoch ist die Wahrscheinlichkeit, dass der Jäger mit mindestens einem erlegten Tier nach Hause geht?
Interaktive Lösungen zum Aufgabenblatt 1
Lösungen zur Aufgabe 1
Lösungshinweise zu dieser Aufgabe
- Ziehen aus einer Urne mit Zurücklegen bedeutet, dass die Wahrscheinlichkeit, eine weiße, schwarze oder graue Kugel zu ziehen, bei jedem Zug gleich bleibt.
- Wenn bei jedem Zug jede Farbe möglich ist, so setzt sich die Menge der möglichen Ergebnisse aus allen möglichen Kombinationen der Farben zusammen.
- Denke daran, dass die Summe der Wahrscheinlichkeiten auf jeder Ebene zusammen 1 ergeben muss.
- Denke daran, dass die Wahrscheinlichkeiten entlang eines Astes multipliziert werden. Die Wahrscheinlichkeiten einzelner Äste, die zu einem Ereignis gehören werden addiert!
Interaktive Lösung – Bearbeite die Aufgaben hier online und du erfährst, ob du die Aufgabe richtig verstanden und gerechnet hast.
Das 🌳 Diagramm:
Vervollständige das Diagramm, indem du die fehlenden Wahrscheinlichkeiten an die richtige Stelle ziehst (Drag and Drop) bis das Diagramm fertig ist.
Die 🎲 Wahrscheinlichkeiten
Aus dem korrekten Baumdiagramm aus der vorherigen Teilaufgabe kannst Du die Wahrscheinlichkeit ablesen, indem du alle Äste des Baums betrachtet, die die Bedingung erfüllen.
Welche Wahrscheinlichkeit ergibt sich an Ende von jedem Ast des Baumes? Ziehe auch hier die Wahrscheinlichkeiten an die richtige Stelle
Die Wahrscheinlichkeiten aus dem Baumdiagramm für alle Ergebnisse (möglichen Äste) kannst du berechnen und hier eingeben:
Die Ergebnismenge Ω
Die Ergebnismenge Ω besteht aus allen möglichen Ergebnissen, die nach zweimaligem Ziehen möglich sind.
Das sind alle Farbkombinationen, die vorkommen können. Hierbei ist noch offen, ob wir die Reihenfolge unterscheiden oder nicht unterscheiden. Hier werden alle Kombinationen mit der Beachtung der Reihenfolge angegeben, das entspricht den Nummern 1 – 9 im Bild nebenan.
Ω = {(weiss, weiss), (schwarz, schwarz), (grau, grau),
(weiss, schwarz), (weiss, grau), (schwarz, grau),
(schwarz, weiss), (grau, weiss), (grau, schwarz)}
Die gesuchten Wahrscheinlichkeiten betragen:
Bedingte Wahrscheinlichkeiten
Die Aufgabe: “Nun wird eine Kugel unter der Bedingung B gezogen: die gezogene Kugel ist nicht weiß.”
Lösungen zur Aufgabe 2
Lösungshinweise
Wir können dieses Experiment mit einem dreistufigen Baumdiagramm darstellen. Auf jeder Ebene gibt es zwei Äste an jedem neuen Endpunkt: weiss oder grau.
Notiere an jedem Ast die Wahrscheinlichkeit und am Ende die Wahrscheinlichkeit für den ganzen Weg.
Zähle dann die Äste bzw. Wege zusammen, die zu einem Gewinn führen.
Zeichne ein Baumdiagramm mit den Wahrscheinlichkeiten. Wenn du es selbst probiert hast, solltest du erst die einzelnen Lösungsschritte aufklappen!
Die Lösungen:
Die weißen Kreise stehen für das Segment, das gewinnt, der graue Kreis steht für eine Niete.
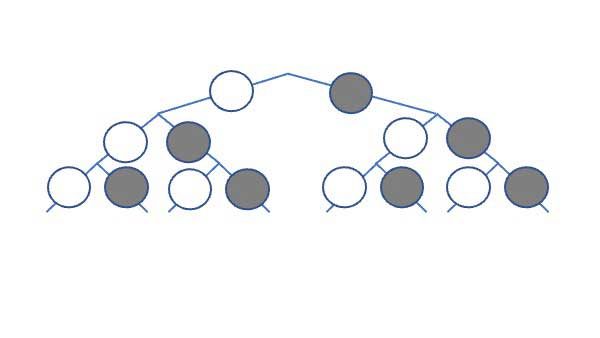
Jetzt kannst du in jeden Kreis die Wahrscheinlichkeit für dieses Ereignis schreiben.
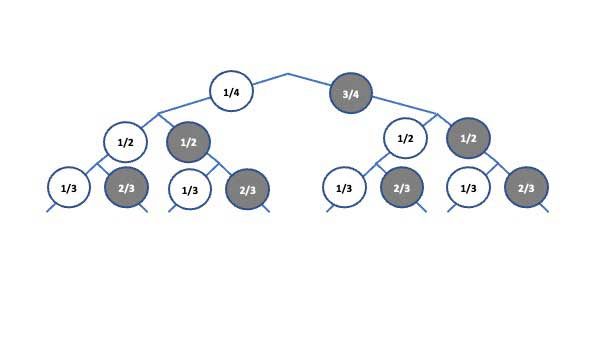
In jedem Kreis findest du jetzt die Wahrscheinlichkeit.
Rot ist der Weg markiert, der zu einem Gewinn von 5 € führt. Grün sind die Wege markiert, die zu einem Gewinn von 3 € führen.
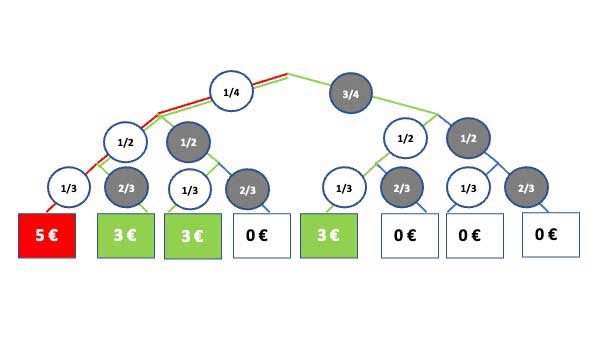
Beachte, dass bei einem Einsatz von 1 € jeder Gewinn um diesen Betrag reduziert werden muss, um den tatsächlichen Gewinn zu erkennen.
Jetzt musst du noch die Wahrscheinlichkeiten für die 3 Möglichkeiten berechnen:
- Rot: 4 € realer Gewinn
- Grün: 2 € realer Gewinn
- Weiss: 1 € Verlust
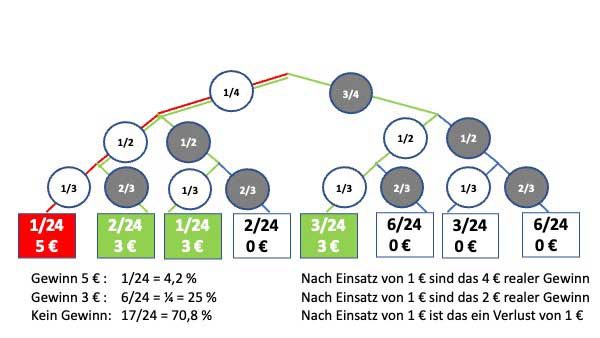
Die Wahrscheinlichkeit für einen Gewinn ergibt sich aus der Summe der Wahrscheinlichkeiten für 5 € und 3 € Gewinn. Diese beträgt etwa 29,2 %.
Die Gewinn und Verlustrechnung:
Bewerte nun selbst, ob sich das Glücksspiel für den Veranstalter des Spiels oder für die Teilnehmer lohnt.
Berücksichtige in deiner Bewertung auch, dass der Veranstalter noch zusätzliche Kosten hat, um Personal und Ausstattung zu bezahlen.
Lösungen zur Aufgabe 3
Lösungshinweise zu dieser Aufgabe
Zunächst sollten wir analysieren, wie viele Schüler aus der Klassenstufe teilnehmen. Daraus ergibt sich ebenfalls die Anzahl der Schüler, die insgesamt an dem Quiz teilnehmen.
Aus diesen Angaben berechnen wir dann den Anteil der Teilnehmer aus der Mittelstufe.
Für den Aufgabenteil b) müssen wir nur die Zahlen der Mittelstufe betrachten.
Lösung zu Teil a) und b)
Lösungen zur Aufgabe 4
Lösungshinweise
Modelliere diese Aufgabe mit einem Baumdiagramm. Wir nehmen an, dass zuerst auf das eine Tier, dann auf das andere Tier geschossen wird. Es handelt sich also um ein mehrstufiges Zufallsexperiment. Dabei ist es unerheblich, ob zuerst auf den Hasen oder zuerst auf das Reh geschossen wird. Wähle in der interaktiven Lösung als ersten Schuss den Schuss auf das Reh.
Jetzt betrachte das Baumdiagramm und finde die Wege, die zu der Aufgabenstellung passen.
Alternativ können wir die Fälle (Wahrscheinlichkeiten) auch ohne Baumdiagramm notieren.
Tipp:
Überlege, ob das Gegenereignis vom gesuchten Ereignis einfacher zu berechnen ist. Falls dies zutrifft, berechne zuerst die Wahrscheinlichkeit für das Gegenereignis. Das gesuchte Ergebnis ist dann “P = 1 – Gegenereignis.”
Vorüberlegung:
Gegenereignis:
Wie lautet das Gegenereignis zu “mindestens einmal treffen”?
Die Rechnung:
Baumdiagramm:
Stelle jetzt das Baumdiagramm mit den Werten für die Wahrscheinlichkeiten auf!
Fahre mit der Maus über das Bild oder klicke es an, um die Lösung zu sehen.
Klicke auf das Bild!
🎲 Arbeitsblätter zur Wahrscheinlichkeitsrechnung
Aufgaben zur Wahrscheinlichkeitsrechnung – Blatt 1
Weitere Aufgabenblätter zu diesem Thema findest du bis zum kompletten Aufbau dieser Seite auch bei der aktuellen Materialseite mit Matheaufgaben von Mathefritz bei Mathe Arbeitsblätter bei Mathestunde.com

 Aufgabenblatt 1 als PDF ausdrucken
Aufgabenblatt 1 als PDF ausdrucken