Drawing linear functions - what are linear functions?
What are Linear Functions?
Linear functions explanation - What are linear functions?
On this page, Mathefritz explains what linear functions are:
To do this, we start with assignments. Then we get into the concept of a function and then we move on to the linear function.
Mathefritz tries to explain the linear function as simply and precisely as possible. You can also find more theoretical information on the topic of "linear function" at Wikipedia!

What are linear functions?
Assignments - Entry
We start with mappings before we understand what linear functions are.
How do linear functions work - to understand this, we first need to look at mappings.
Examples of assignments in everyday life
Example 1:
Peter buys walnuts at the fruit shop. One kilogram costs 4 €. How much do 200 g, 500g, 1.2 kg cost?
Example 2:
In a multi-storey car park, parking costs €1 per half hour or part thereof. From 2 hours, the half hour costs only €0.75. Parking for longer than 4 hours in one day costs a flat rate of €7.50 (i.e. for the whole day).
Calculate the parking fee for 10 minutes, for 50 minutes, for 2 hours 20 minutes, for 6 hours 15 minutes.
Example 3:
The Meyers family has 4-minute eggs for breakfast every Sunday.
How long does it take to cook 2, 3 or 5 eggs?
Notice:
In these examples, values are always assigned to each other:
- The quantity of walnuts is assigned the price for them.
- A parking fee is assigned to the parking duration.
- The eggs are assigned a cooking time.
In order to present such assignments more clearly and to answer the questions in the examples, there are various possibilities. One of them is the value table.
Value tables - on the way to linear functions
Our example 1:
kg walnuts | 1 kg = 1000g | 100 g | 200 g | 500 g = 0.5 kg | 1.2 kg =1200 g |
Price in € | 4 € | 0,40 € | 0,80 € | 2,00 € | 4,80 € |
In order to easily calculate the prices for 200 g, 500 g and 1.2 kg, it is helpful to first note the price for a small quantity, here for example for 100 g. This is already an example of a table of values for linear functions.
Example 2:
Parking time | 0.5 h = 30 min | 10 min | 50 min | 2h 20min | 6h 15min |
Parking fee | 1 € | 1 € | 1€+1€ = 2 € | 4 x 1€ + 0,75€ = 4,75 € | 7,50 € |
In order to calculate the parking fees, it should be noted that they do not change evenly, but "jump".
Example 3:
Number of eggs | 1 Egg | 2 eggs | 3 eggs | 5 eggs | 10 eggs |
Cooking time in min | 4 min | 4 min | 4 min | 4 min | 4 min |
All eggs are ready at the same time, because all eggs have the same time to be cooked.
Diagrams
The assignments can also be represented graphically in a chart. To do this, the values are drawn in a coordinate system. You can then also read off other values.
The walnut example - our example 1 as a diagram
What does 800 g of walnuts cost? This graphical allocation is already a linear function as a chart!
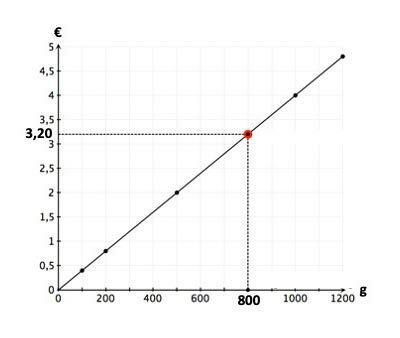
800 g walnuts cost €3.20!
The car park example - Example 2 as a diagram
What is the price in the parking garage for 1:15 h parking?
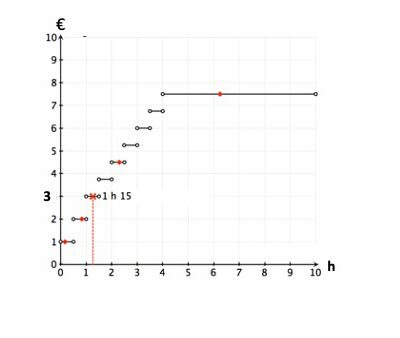
1:15 parking costs €3!
Cooking eggs - Our example 3
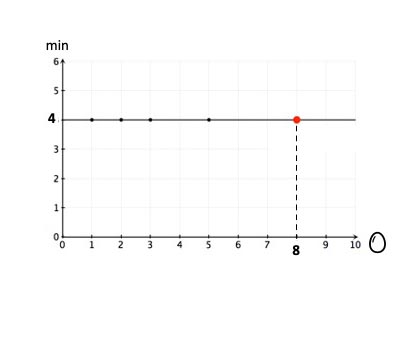
Also 8 eggs have exactly 4 minutes cooking time!
Such assignments are also called functions. With functions, exactly oney value (e.g. y €) is assigned to a certain x value (e.g. x kg).
In a graph , functions are represented by corresponding lines. These are called the graph of the function.
Linear functions Slope
linear function - the slope
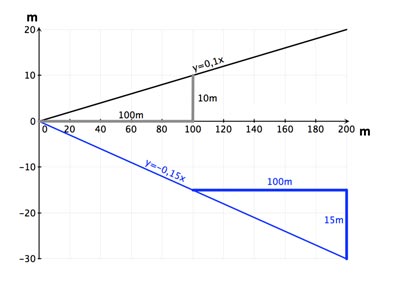
In the example with the walnuts you can see: If twice as many nutsThe gradient triangle - An example
In the mountains, you will often find road signs indicating the gradient or slope of the road. For example, 10 % means that a road rises by 10 m for 100 m of horizontal distance.
In the diagram of a proportional function, one can determine the slope factor or the slope with a slope triangle.

of a linear function
Further examples - gradient and graph of the linear function
So you can draw linear functions if you know the slope.
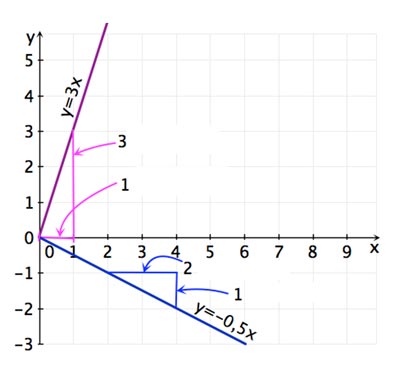
Example 1:
The slope in this functional equation
means: go 2 to the right and 1 down. Downwards because of the minus sign -1!
The straight line goes through the points (0;0) and (2;-1).
Example 2:
Go 1 to the right and 3 up to the point (1;3).
The definition of a linear function
Example for introduction
With her electric bike, Nikki can ride 40 km on one battery charge. If she rides smoothly, she will have used a quarter of the battery's charge after 10 km, so she still has 30 km "reserve".
To draw the diagram for this, we first create a table of values:
| x: Battery consumption | 0 | 1/4 | 1/2 | 3/4 | 1 |
| y: possible distance | 40 km | 30 km | 20 km | 10 km | 0 km |
The points all lie on a straight line.
The gradient is obtained with the gradient triangle:
\)
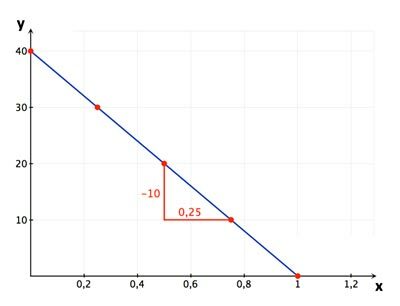
The straight line does not go through the origin of the coordinate system, but is shifted upwards by 40. This results in the equation of a straight line:
\( y = -40 \cdot x + 40 \)
Definition linear function
The mathematical definition:
The function
f(x): x \mapsto m \cdot x + n
\)
is called a linear function with
m, n \in \mathbb{R} .
\)
Every linear function has a straight line as a graph with the slope m and the y-axis intercept n.
To the linear function f(x) belongs the function equation
f(x) = m\cdot x + n
\)
or also:
y = m\cdot x + n
\)
Or the short version:
A function with a straight line equation of the form:
f(x) = m∙x+n
is called a linear function.
Did you get it - test your knowledge!
Draw linear functions online
and the y-axis intercept n
of a linear function!
How do you draw linear functions?
If you know the slope of the straight line (linear function) and the y-intercept (the value when passing through the y-axis), you can draw the graph of the linear function.
We name the slope m and the y-axis intercept n.
Try changing the parameters for the slope m and the y-axis intercept n in the interactive window below. Look closely at how the course of the straight line changes.
- m is the slope of the linear function (straight line).
- n is the y-axis intercept of the line, which is the distance on the y-axis at the point of intersection from the origin
- f: y = m x + n is the function equation, the equation of the linear function!
Tutorial - Draw linear functions:
- Use the slider for the slope and the slider for the y-axis intercept.
- Change the values and follow how the equation for the function f changes in the line below.
- You can use the mouse (or your finger on a tablet computer or smartphone) to move and zoom the displayed area.
