Reduce and expand fractions - worksheets online calculation
Reducing and expanding fractions explained simply
What is meant by reducing and extending fractions?
We start with an exercise to get you started!
We have divided a rectangle in the picture next to it once into 8 parts and once only into 4 parts. Each time, however, the same area is coloured in yellow. How many fractions are there in each case?
Complete the fraction problem under the picture!
Solve the following interactive tasks. Then you will understand better that two different fractions can have the same value. We will now examine this transformation in more detail. It is also called reducing and expanding fractions.
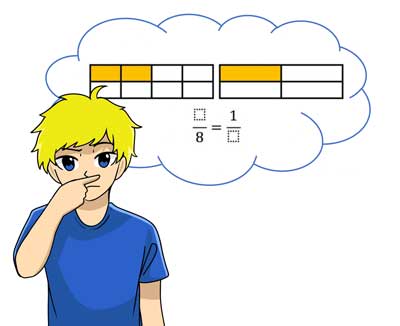
Exercise 1
Add the fractions so that they accurately describe the pictures above!
To do this, drag the matching numbers into the spaces provided!
Extend fractions
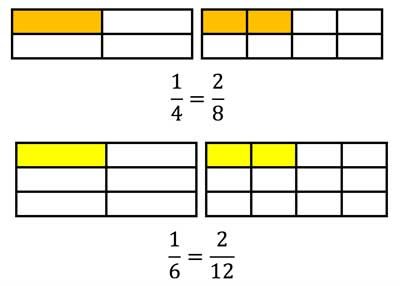
In the picture above we learn to extend fractions with 2
(Each fraction is halved in the process!)
Numerator and denominator are each multiplied by 2!
\(\frac{1}{4}=\frac{1\cdot 2}{4\cdot 2}=\frac{2}{8} \)
\(\frac{1}{6}=\frac{1\cdot 2}{6\cdot 2}=\frac{2}{12} \)
Definition - Extend fractions
Extending a fraction means that we multiplythe numerator and denominator of the fraction by the same number.
Invisual terms, extending means that we continue to divide the fractions all in the same way.
Expand fractions Examples:
\(\frac{1}{3}=\frac{1\cdot 2}{3\cdot 2}=\frac{2}{6}=\frac{2\cdot 3}{6\cdot 3}=\frac{6}{18}\)
\(\frac{3}{8}=\frac{3\cdot 2}{8\cdot 2}=\frac{6}{16}=\frac{6\cdot 3}{16\cdot 3}=\frac{18}{48}\)
\(\frac{2}{5}=\frac{2\cdot 2}{5\cdot 2}=\frac{4}{10}=\frac{4\cdot 3}{10\cdot 3}=\frac{12}{30}\)
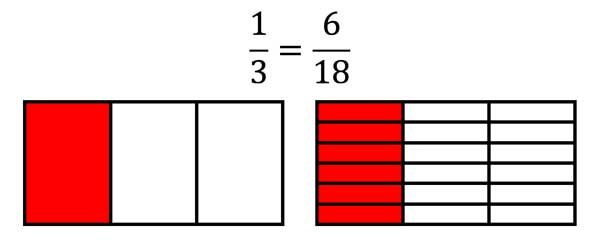
Here, each piece is again divided into 6 parts.
This means expand with 6!
Reduce fractions
Definition - Reducing fractions
Shortening a fraction means that we divide the numerator and denominator of the fraction by the same number.
REMINDER!
If we can no longer divide the numerator and denominator of a fraction by an equal number, we speak of the fraction being completely truncated.
In order for us to be able to divide the numerator and denominator of a fraction by the same number, we have to check very carefully by which numbers the numerator and denominator are divisible at all. To do this, we have to use the Be able to apply divisibility rules and the prime factorization!
Shorten fractions Examples:
\(\frac{6}{18}=\frac{6:3}{18:3}=\frac{2}{6} =\frac{2:2}{6:2}=\frac{1}{3} \)
\(\frac{42}{60}=\frac{42:6}{60:6}=\frac{7}{10} \)
\(\frac{48}{80}=\frac{48:8}{80:8}=\frac{6}{10} =\frac{6:2}{10:2}=\frac{3}{5} \)
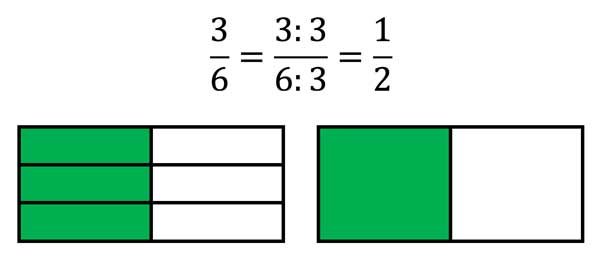
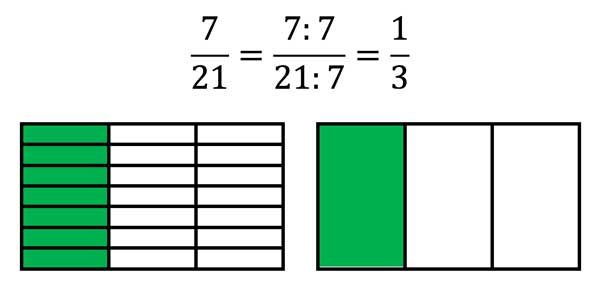
In the pictures above we learn to shorten fractions by 3 and by 7.
Always 3 or always 7 parts are combined into one part. Of course, this only works if the total number of all parts is divisible by 3 or by 7.
The prime factorisation to reduce fractions
Reducing fractions becomes particularly easy if we divide the numerator and denominator of the fraction into Decomposing prime factors. Then we can simply cross out common factors in the numerator and denominator. We shorten fractions completely with this method!
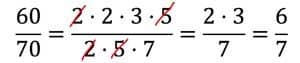
If you still have problems with the prime factorisation, visit our page on divisibility and prime factorisation and use the online calculator for prime factorisation!
Did you understand the method of complete shortening with the prime factorization?
Do the little online exercise to test it!
Proceed as follows:
- Decompose the numerator and denominator into prime factors!
- Leave out common factors!
- Enter all remaining factors again!
- Always write down the numbers in ascending order (from small to large).
Shorten and expand fractions - online exercises
We practise expanding fractions!
Note the note on filling in:
Enter the value for the numerator for A and the value for the denominator for B in the empty fields. Unfortunately, the online tool for the task cannot display this input directly on or below the fraction line!
Example - This is how you calculate the tasks in the online exercise:
\( \frac{1}{2} \overset{ \cdot \text{10}}{=} \frac{A}{B}\) A = 10 B = 20\( \frac{12}{15} \underset{ \text{:3}}{=} \frac{A}{B}\) A = 4 B = 5Exercise 1 - Expand fractions
a) Expand all fractions with 3!
b) Expand all fractions with 5!
c) Expand all fractions with 8!
Exercise 2 - Shortening fractions - simple
Brevity ONLY with the number given under the equal sign!
a) Short the fraction with the greatest common divisor.
In this task a) the common divisor is still under the equal sign!
b) Completely shorten so that the numerator and denominator no longer have a common divisor!
Only completely shortened is the result correct!
c) Completely shorten so that the numerator and denominator no longer have a common divisor!
d) Completely shorten so that the numerator and denominator no longer have a common divisor!
Memo games: Find equal fractions reduced or expanded
Memo games - shorten and expand fractions
Find fractions with the same value! To do this, you have to expand or shorten a fraction to find an equivalent fraction.
Memo game 1
The book with many fraction tasks: "Maths lesson 5 - Simple fractions".
The exercise book for getting started with fractions, many tasks on shortening and expanding fractions in one booklet!
Maths lesson 5 - Simple fractions
Exercise book for 5th grade / 6th grade
- Length: 60 pages, DIN A 4, stitched, b/w
- Published: 2015
- ISBN: 978-394186817-5
- Price: 5,95 €
- Available everywhere in every bookshop (orderable) or in online shops.

